
����Ŀ���������ǵ�����ˮƽ������ߣ�����Խ��Խע������Ʒ�ʣ�ע��ʳ��Ӫ����ˮ����ͷ�ڱ����ʶȺ�Ӫ������������������ժˮ����ˮ����ͷ��������óԣ�ˮ���ı�ɫ��ζ��ȫ���뵽��ˮ�У���ͷˮ�ķ�ζ�����ȹ�֭��ҪŨ����ij���������Լס�������ˮ��Ϊԭ�ϵ�ij�ֹ�ͷ����һ�ν����е�֪������1.8��Ԫ�����ļ���ˮ����2.4��Ԫ����������ˮ��������ͬ������ˮ��ÿǧ�˱ȼ���ˮ����2Ԫ��
��1����ס�������ˮ���ĵ��ۣ�
��2�����佫ˮ���Ƴɹ�ͷͶ���г�������������֪һ����ͷ��Ҫ����ˮ����0.5ǧ�ˣ���ÿ����ͷ�ijɱ�����ˮ���ɱ�֮�⣬�������гɱ���ˮ���ɱ���![]() �Ļ�Ҫ��3Ԫ�����鷢�֣���28Ԫ�Ķ��۽������ۣ�ÿ��ֻ������3000�������ж������д�����ÿ����1Ԫ��ƽ��ÿ��ɶ�����1000�������ۼ�Ϊ����Ԫʱ����������������Ϊ���٣�
�Ļ�Ҫ��3Ԫ�����鷢�֣���28Ԫ�Ķ��۽������ۣ�ÿ��ֻ������3000�������ж������д�����ÿ����1Ԫ��ƽ��ÿ��ɶ�����1000�������ۼ�Ϊ����Ԫʱ����������������Ϊ���٣�
��3������ʹ�ø��ֹ�ͷ����������ÿ��ﵽ6��Ԫ�����ұ�֤���۵ķ��Ȳ��������۵�15%��ÿ����ͷ�ļ�ǮӦΪ����Ǯ��
���𰸡���1���ĵ���Ϊ6Ԫ/ǧ�ˣ��ҵĵ���Ϊ8Ԫ/ǧ�ˣ���2�����ۼ�Ϊ23Ԫʱ���������Ϊ64000����3���ۼ�Ϊ25Ԫʱ������Ϊ6��Ԫ
��������
��1�����������ϵΪ������ˮ������=����ˮ���ĵ���+2�����ݻ���1.8��Ԫ�����ļ���ˮ����2.4��Ԫ����������ˮ��������ͬ����δ֪�����з��̣�Ȼ��������̵Ľ�.��2�������ÿ����ͷ���ܳɱ����轵��mԪ����������ɵõ�������W��m�ĺ�������ʽ���ٽ���������ʽת��Ϊ����ʽ��Ȼ�����ö��κ��������ʿ����.��3�����ã�2����w=60000����������m�ķ��̣��ⷽ�����m��ֵ�����ɽ������.
��1�������ˮ���ĵ���Ϊ![]() Ԫ/ǧ�ˣ�������ˮ���ĵ���Ϊ
Ԫ/ǧ�ˣ�������ˮ���ĵ���Ϊ![]() Ԫ/ǧ�ˣ�
Ԫ/ǧ�ˣ�
������ɵã�![]() ,
,
��ã�![]() ,
,
�����飬![]() Ϊ���̵ĸ��ҷ�������,
Ϊ���̵ĸ��ҷ�������,
��![]() ,
,
![]() �ĵ���Ϊ6Ԫ/ǧ�ˣ��ҵĵ���Ϊ8Ԫ/ǧ�ˣ�
�ĵ���Ϊ6Ԫ/ǧ�ˣ��ҵĵ���Ϊ8Ԫ/ǧ�ˣ�
��2���ɣ�1��ÿ����ͷ��ˮ���ɱ�Ϊ��![]() Ԫ��
Ԫ��
���⣬ÿ����ͷ���ܳɱ�Ϊ![]() Ԫ��
Ԫ��
�轵��![]() Ԫ��������
Ԫ��������![]()
![]()
![]()
![]() ��
��
![]() ��
��![]() ʱ��
ʱ��![]() �����ֵΪ64000��
�����ֵΪ64000��
![]() ���ۼ�Ϊ23Ԫʱ���������Ϊ64000��
���ۼ�Ϊ23Ԫʱ���������Ϊ64000��
��3���ɣ�2���ã�![]() ��
��
��ã�![]() ��3��
��3��
���ǣ����۷��Ȳ��������۵�15%����![]() ��28��15%��
��28��15%��
![]() ��
��
![]() ��
��
![]() �ۼ�Ϊ
�ۼ�Ϊ![]() ��
��
���ۼ�Ϊ25Ԫʱ������Ϊ6��Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
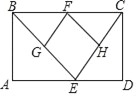
����Ŀ����֪����ABCD�У�E��AD���ϵ�һ�����㣬��F��G��H�ֱ���BC��BE��CE���е㣮
��1����֤����BGF�ա�FHC��
��2����AD=a�����ı���EGFH��������ʱ�������ABCD�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У���AB��CD�ཻ�ڵ�E��
�У���AB��CD�ཻ�ڵ�E��![]() ��
��![]() ����D��
����D��![]() �ϣ�����CO�����ӳ�CO���߶�AB�ڵ�F������OA��OB����OA��2����OBA��30��
�ϣ�����CO�����ӳ�CO���߶�AB�ڵ�F������OA��OB����OA��2����OBA��30��
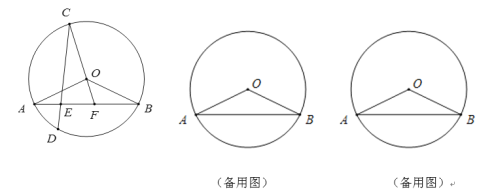
��1����֤����OBA����OCD��
��2����![]() AOF��ֱ��������ʱ����EF�ij���
AOF��ֱ��������ʱ����EF�ij���
��3���Ƿ���ڵ�F��ʹ��![]() �������ڣ������EF�ij����������ڣ���˵������.
�������ڣ������EF�ij����������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ƕ����������ཻ�ĺ���ͼ������ֱ�����ϵ���̾���Ϊ�����������ġ���гֵ����
(1)��������y��x2��2x+2��x��ġ���гֵ����
(2)��������y��x2��2x+2��ֱ��y��x��1�ġ���гֵ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
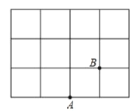
����Ŀ����ͼ����ÿ��С�����εı߳�Ϊ1������ͼ���У�ÿ��С�����εĶ����Ϊ��㣬�������������ɵ���������������С��1���Ϊ������������������������ǡ�õ���1���Ϊ����������������![]() ������ͼ������֪��������㣬��
������ͼ������֪��������㣬��![]() ����һ����㣬������
����һ����㣬������![]() ��������������������
��������������������![]() �����������������ĸ�����__________��
�����������������ĸ�����__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����λͬѧ���о�����y=x2+bx+c(b��c�dz���)ʱ�����ֵ�x=1ʱ����������Сֵ���ҷ��֩�1�Ƿ���x2+bx+c=0��һ�����������ֺ�������СֵΪ3�������ֵ�x=2ʱ��y=4����֪����λͬѧ��ֻ��һλ���ֵĽ����Ǵ���ģ����ͬѧ��( )
A. �� B. �� C. �� D. ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ѧ��ȤС���Сӱ�������ѧ¥ǰ��һ���������ߣ��������ʱ�����һ����Ϊ1m����͵�Ӱ����0��8m�����������ϲ�������ʱ����������Ӱ�Ӳ�ȫ���ڵ����ϣ���һ����Ӱ�����ڽ�ѧ¥��ǽ���ϣ���ͼ�������Ȳ������ǽ���ϵ�Ӱ��Ϊ1��2m���ֲ�õ����Ӱ��Ϊ2��6m�����������һ�£������ǣ� ��
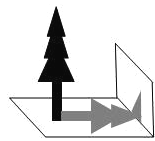
A��3��25m B��4��25m C��4��45m D��4��75m
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
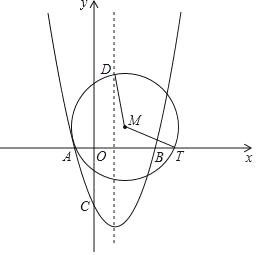
����Ŀ����ͼ�����κ���y��x2+bx��3��ͼ����x��ֱ��ཻ��A��B��������B������Ϊ��3��0������y��Ľ���ΪC������T������AB���˶����������ߵĶԳ���l����һ����D����������Ϊ2![]() ��l��x��Ľ���ΪE������A��T��D��������M��
��l��x��Ľ���ΪE������A��T��D��������M��
��1������κ����ı���ʽ��
��2���ڵ�T���˶������У�
����DMT�Ķ����Ƿ�Ϊ��ֵ�����ǣ�������ö�ֵ�������ǣ���˵�����ɣ�
����MT��![]() AD�����M�����ꣻ
AD�����M�����ꣻ
��3��������T������EB���˶�ʱ������M��MH��x���ڵ�H����HT��a����OH��x��OTʱ����y�����ֵ����Сֵ���ú�a��ʽ�ӱ�ʾ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪Rt��ABC����BAC��90����BC��5��AC��2![]() ����AΪԲ�ġ�ABΪ�뾶��Բ�����BC������һ��D��
����AΪԲ�ġ�ABΪ�뾶��Բ�����BC������һ��D��
��1����BD�ij���
��2������AD�����DAC������ֵ��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com