
【题目】如图,在△ABC中,AD平分∠BAC,按如下步作图:①分别以点A,D为圆心,以大于![]() AD的长为半径在AD两侧作弧,两弧交于两点M,N;②作直线MN分别交AB,AC于点E,F;③连接DE,DF,若BD=6,AE=4,CD=3,则CF的长是( )
AD的长为半径在AD两侧作弧,两弧交于两点M,N;②作直线MN分别交AB,AC于点E,F;③连接DE,DF,若BD=6,AE=4,CD=3,则CF的长是( )
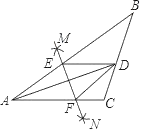
A.1B.1.5C.2D.3
科目:初中数学 来源: 题型:
【题目】如图,是一座古拱桥的截面图,拱桥桥洞的上沿是抛物线形状,当水面的宽度为10m时,桥洞与水面
的最大距离是5m.
(1)经过讨论,同学们得出三种建立平面直角坐标系的方案(如下图)
你选择的方案是_____(填方案一,方案二,或方案三),则B点坐标是______,求出你所选方案中的抛物线的表达式;
(2)因为上游水库泄洪,水面宽度变为6m,求水面上涨的高度.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中AC,BD相交于点O,点E是OA的中点,连接BE并延长AD于点F,已知△AEF的面积=1,则平行四边形ABCD的面积是( )
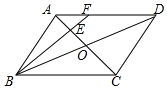
A.24B.18C.12D.9
查看答案和解析>>
科目:初中数学 来源: 题型:
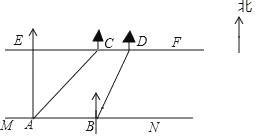
【题目】在社会实践课上,小聪所在小组要测量一条小河的宽度,如图,河岸EF∥MN,小聪在河岸MN上的点A处测得河对岸小树C位于东北方向,然后向东沿河岸走了30米,到达B处测得河对岸小树D位于北偏东30°的方向,又有同学测得CD=10米
(1)∠EAC= 度,∠DBN= 度;
(2)求小河的宽度AE.(结果精确到0.1米,参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
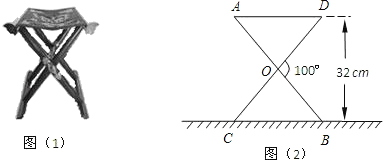
【题目】某大学计划为新生配备如图(1)所示的折叠椅.图(2)是折叠椅撑开后的侧面示意图,其中椅腿AB和CD的长相等,O是它们的中点.为使折叠椅既舒适又牢固,厂家将撑开后的折叠椅高度设计为32cm,∠DOB=100°,那么椅腿的长AB和篷布面的宽AD各应设计为多少cm?(结果精确到0.1cm)
查看答案和解析>>
科目:初中数学 来源: 题型:
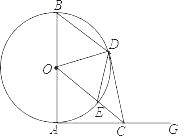
【题目】如图,AB为⊙O的直径,射线AG为⊙O的切线,点A为切点,点C为射线AG上任意一点,连接OC交⊙O于点E,过点B作BD∥OC交⊙O于点D,连接CD,DE,OD.
(1)求证:△OAC≌△ODC;
(2)①当∠OCA的度数为 时,四边形BOED为菱形;
②当∠OCA的度数为 时,四边形OACD为正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的三个顶点和点O都在正方形网格的格点上,每个小正方形的边长都为1.
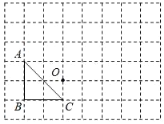
(1)将△ABC先向右平移4个单位,再向上平移2个单位得到△A1B1C1,请画出△A1B1C1;
(2)请画出△A2B2C2,使△A2B2C2和△ABC关于点O成中心对称.
查看答案和解析>>
科目:初中数学 来源: 题型:
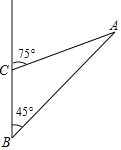
【题目】成都市第十三次党代会提出实施“东进”战略,推动了城市发展格局“千年之变”成都龙泉山城市森林公园借“东进”之风,聚全市之力,着力打造一个令世界向往的城市中心,如图为成都市龙泉山城市豪林公园三个景点A,B,C的平面示意图,景点C在B的正北方向5千米处,景点A在B的东北方向,在C的北偏东75°方向上.
(1)∠BAC的大小
(2)求景点A,C的距离(![]() =1.414,
=1.414,![]() =1.732,sin75°≈0.966,cos75°≈0.259,tan75°≈3.732,结果精确到0.1)
=1.732,sin75°≈0.966,cos75°≈0.259,tan75°≈3.732,结果精确到0.1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点F从菱形ABCD的顶点A出发,沿A→D→B以1cm/s的速度匀速运动到点B,图2是点F运动时,△FBC的面积y(cm2)随时间x(s)变化的关系图象,则a的值为( )

A. ![]() B. 2 C.
B. 2 C. ![]() D. 2
D. 2![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com