
【题目】如图,正方形ABCD中,E是BC的中点,F为CD上一点,CD=4CF,下列结论:
(1)∠BAE=30°;
(2)AE⊥EF;
(3)AE=2EF,其中正确的个数为( )
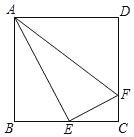
A.0个B.1个C.2个D.3个
【答案】C
【解析】
根据正方形性质、相似三角形应用以及三角函数逐一求证即可
解:如图所示:
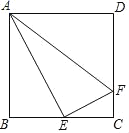
(1))∠BAE=30°是错误的,其原因如下:
∵四边形ABCD是正方形,
∴AB=BC=CD,∠B=∠C=90°
又∵E是BC的中点,
∴BE=CE=![]() BC=
BC=![]() AB,
AB,
又∵在Rt△ABE中,tan∠BAE=![]() =
=![]() ,
,
tan30°=![]() ,
,
∴![]()
∴∠BAE<30°,
∴(1)不正确;
(2)AE⊥EF是正确的,其原因如下:
∵CD=4CF,
∴CD=2CE,
∵![]() ,∠B=∠C=90°,
,∠B=∠C=90°,
∴△ABE∽△ECF,
∴∠BAE=∠CEF,
又∵∠BAE+∠AEB=90°,
∴∠AEB+∠CEF=90°,
又∵∠BEA+∠AEF+∠CEF=180°,
∴∠AEF=90°,
∴AE⊥EF,
∴(2)正确.
(3)AE=2EF正确,其原因如下:
∵由(2)可知△ABE∽△ECF,
∴![]()
∴AE=2EF,
所以③正确;
综合所述,(2)(3)正确.
故选:C.


科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代第一部自成体系的数学专著,代表了东方数学的最高成就.它的算法体系至今仍在推动着计算机的发展和应用.书中记载:“今有圆材埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”译为:“今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯这木材,锯口深1寸(ED=1寸),锯道长1尺(AB=1尺=10寸)”,问这块圆形木材的直径是多少?”
如图所示,请根据所学知识计算:圆形木材的直径AC是( )
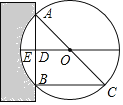
A. 13寸 B. 20寸 C. 26寸 D. 28寸
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,则图中阴影部分的面积是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,∠B=90°,AB=5cm,BC=7cm.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.
(1)如果P,Q分别从A,B同时出发,那么几秒后,△PBQ的面积等于6cm2?
(2)在(1)中,△PQB的面积能否等于8cm2?说明理由.
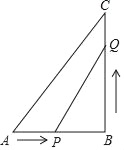
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读资料:我们把顶点在圆上,并且一边和圆相交、另一边和圆相切的角叫做弦切角,如下左图∠ABC所示。
同学们研究发现:P为圆上任意一点,当弦AC经过圆心O时,且AB切⊙O于点A,此时弦切角∠CAB=∠P(图甲)
证明:∵AB切⊙O于点A, ∴∠CAB=90°, 又∵AC是直径, ∴∠P=90° ∴∠CAB=∠P

问题拓展:若AC不经过圆心O(如图乙),该结论:弦切角∠CAB=∠P还成立吗?
请说明理由。
知识运用:如图,AD是△ABC中∠BAC的平分线,经过点A的⊙O与BC切于点D,与AB、AC分别相交于E、F。 求证:EF∥BC。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将长方形ABCD沿着对角线BD折叠,使点C落在![]() 处,
处,![]() 交AD于点E.
交AD于点E.
(1)试判断△BDE的形状,并说明理由;
(2)若![]() ,
,![]() ,求△BDE的面积.
,求△BDE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,△ABC和△DEF相似,则关于位似中心与相似比叙述正确的是( )

A. 位似中心是点B,相似比是2:1 B. 位似中心是点D,相似比是2:1
C. 位似中心在点G,H之间,相似比为2:1 D. 位似中心在点G,H之间,相似比为1:2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,BD是AC边上的中线,AE⊥BC,垂足为点E,交BD于F,cos∠ABC=![]() ,AB=13.
,AB=13.
(1)求AE的长;
(2)求tan∠DBC的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com