
【题目】在同一坐标系中,函数y=![]() 和y=﹣kx+3的大致图象可能是( )
和y=﹣kx+3的大致图象可能是( )
A.  B.
B.  C.
C.  D.
D. 
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系中的任意两点![]() ,
,![]() ,我们把
,我们把![]() 叫
叫![]() ,
,![]() 两点间的“平面距离”,记作
两点间的“平面距离”,记作![]() .
.
(![]() )已知
)已知![]() 为坐标原点,动点
为坐标原点,动点![]() 是坐标轴上的点,满足
是坐标轴上的点,满足![]() ,请写出点
,请写出点![]() 的坐标.答:__________.
的坐标.答:__________.
(![]() )设
)设![]() 是平面上一点,
是平面上一点,![]() 是直线
是直线![]() 上的动点,我们定义
上的动点,我们定义![]() 的最小值叫做
的最小值叫做![]() 到直线
到直线![]() 的“平面距离”.试求点
的“平面距离”.试求点![]() 到直线
到直线![]() 的“平面距离”.
的“平面距离”.
(![]() )在上面的定义基础上,我们可以定义平面上一条直线
)在上面的定义基础上,我们可以定义平面上一条直线![]() 与⊙
与⊙![]() 的“直角距离”:在直线
的“直角距离”:在直线![]() 与⊙
与⊙![]() 上各自任取一点,此两点之间的“平面距离”的最小值称为直线
上各自任取一点,此两点之间的“平面距离”的最小值称为直线![]() 与⊙
与⊙![]() 的“平面距离”,记作
的“平面距离”,记作![]() .
.
试求直线![]() 与圆心在直线坐标系原点、半径是
与圆心在直线坐标系原点、半径是![]() 的⊙
的⊙![]() 的直角距离
的直角距离![]() __________.(直接写出答案)
__________.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙三位运动员在相同条件下各射靶![]() 次,每次射靶的成绩如下:
次,每次射靶的成绩如下:
甲:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
乙:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
丙:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
(1)根据以上数据完成下表:
平均数 | 中位数 | 方差 | |
甲 |
|
| __________ |
乙 | __________ |
|
|
丙 |
| __________ |
|
(2)根据表中数据分析,哪位运动员的成绩最稳定.并简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
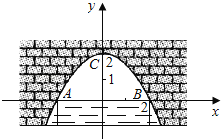
【题目】图中是抛物线形拱桥,当拱顶离水面2m时,水面宽4m,建立如图所示的平面直角坐标系:
(1)求拱桥所在抛物线的解析式;
(2)当水面下降1m时,则水面的宽度为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1是一个重要公式的几何解释.请你写出这个公式: ;
(2)如图2,已知![]() ,
,![]() ,且
,且![]() 三点共线.
三点共线.
试证明![]() ;
;

(3)勾股定理是几何学中的明珠,千百年来,人们对它的证明趋之若骛,有资料表明,关于勾股定理的证明方法已有500余种.课本中介绍了比较有代表性的赵爽弦图.
伽菲尔德(Garfield,1881年任美国第20届总统)利用图2证明了勾股定理(1876年4月1日,发表在《新英格兰教育日志》上),请你写出该证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△OAB的边长为2,点B在x轴上,反比例函数的图象经过A点,将△OAB绕点O顺时针旋转α(0°<α<360°),使点A落在双曲线上,则α=________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点D为
,点D为![]() 的中点,直角
的中点,直角![]() 绕点D旋转,
绕点D旋转,![]() ,
,![]() 分别与边
分别与边![]() ,
,![]() 交于E,F两点,下列结论:①
交于E,F两点,下列结论:①![]() 是等腰直角三角形;②
是等腰直角三角形;②![]() ;③
;③![]() ;④
;④![]() ,其中正确结论是( ).
,其中正确结论是( ).

A.①②④B.②③④C.①②③D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1:y=﹣![]() x与反比例函数y=
x与反比例函数y=![]() 的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2:
的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2:
(1)求反比例函数的表达式;
(2)将直线l1:y=﹣![]() x向上平移后的直线l2与反比例函数y=
x向上平移后的直线l2与反比例函数y=![]() 在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.
在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 为等边三角形,
为等边三角形,![]() 为射线
为射线![]() 上一点,
上一点,![]() 为射线
为射线![]() 上一点,
上一点,![]() .
.
(1)如图1,当点![]() 在
在![]() 的延长线上且
的延长线上且![]() 时,
时,![]() 是
是![]() 的中线吗?请说明理由;
的中线吗?请说明理由;
(2)如图2,当点![]() 在
在![]() 的延长线上时,写出
的延长线上时,写出![]() 之间的数量关系,请说明理由;
之间的数量关系,请说明理由;
(3)如图3,当点![]() 在线段
在线段![]() 的延长线上,点
的延长线上,点![]() 在线段
在线段![]() 上时,请直接写出
上时,请直接写出![]() 的数量关系.
的数量关系.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com