
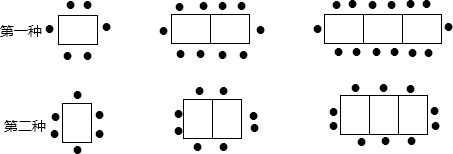
分析 (1)在第一、二两种摆放方式中,桌子数量增加时,左右两边人数不变,每增加一张桌子,上下增加4人、2人,据此规律列式即可;
(2)首先判断按某一种方式摆放不能满足需要,再分类讨论两种方式混用时的情况.
解答 解:(1)第一种:1张桌子可坐人数为:2+4;2张桌子可坐人数为:2+2×4;3张桌子可坐人数为:2+3×4;
故当有n张桌子时,能坐人数为:2+n×4,即4n+2人;
第二种:1张桌子能坐人数为:4+2;2张桌子能坐人数为:4+2×2;3张桌子能坐人数为:4+3×2;
故当有n张桌子时,能坐人数为:4+n×2,即2n+4人.
(2)因为设4n+2=52,解得n=12.5.n的值不是整数.
2n+4=52,解得n=24>13.
所以需要两种摆放方式一起使用.
①若13张餐桌全部使用:
设用第一种摆放方式用餐桌x张,则由题意可列方程4x+2+2(13-x)+4=52.
解得x=10.
则第二种方式需要桌子:13-10=3(张).
②若13张餐桌不全用.当用11张按第一种摆放时,4×11+2=46(人).
而52-6=6(人),用一张餐桌就餐即可.
答:当第一种摆放方式用10张,第二种摆放方式用3张,或第一种摆放方式用11张,再用1张餐桌单独就餐时,都能恰好让顾客坐满席.
故答案为:(1)4n+2,2n+4.
点评 本题考查了图形的变化,通过生活中实际例子,考查学生的观察能力和解决问题能力.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 直线y=x+b与x轴交于点C(4,0),与y轴交于点B,并与双曲线y=$\frac{m}{x}$(x<0)交于点A(-1,n).
直线y=x+b与x轴交于点C(4,0),与y轴交于点B,并与双曲线y=$\frac{m}{x}$(x<0)交于点A(-1,n).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC中,DE∥BC,若AD:DB=2:3,则下列结论中正确的( )
如图,△ABC中,DE∥BC,若AD:DB=2:3,则下列结论中正确的( )| A. | $\frac{DE}{BC}$=$\frac{2}{3}$ | B. | $\frac{DE}{BC}$=$\frac{2}{5}$ | C. | $\frac{AE}{AC}$=$\frac{2}{3}$ | D. | $\frac{AE}{EC}$=$\frac{2}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com