
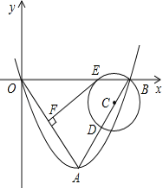
【题目】如图,平面直角坐标系中点A坐标为(2,﹣4),以A为顶点的抛物线经过坐标原点交x轴于点B.
(1)求抛物线的解析式;
(2)取线段AB上一点D,以BD为直径作⊙C交x轴于点E,作EF⊥AO于点F,
求证:EF是⊙C的切线;
(3)设⊙C的半径为r,EF=m,求m与r的函数关系式及自变量r的取值范围.
【答案】(1)y=x2﹣4x;(2)证明见解析;(3) ![]() .
.
【解析】
(1)结合已知条件可以知道抛物线经过A(2,-4),O(0,0),代入解析式,即可求出抛物线的解析式;
(2)连接CE,只要求证CE∥AO,结合已知推出EF⊥CE,即可求证出结论;
(3)作AH⊥OB于H点,结合勾股定理和抛物线的性质求出个线段的长度,根据平行线的性质,写出比例式,求出半径CB的长度
(1)设y=a(x﹣2)2﹣4,把O(0,0)代入,得4a﹣4=0,
∴a=1,
∴y=(x﹣2)2﹣4=y=x2﹣4x;
(2)连接CE,
∴CE=CB
∴∠CEB=∠CBE
∵抛物线有对称性
∴AO=AB
∴∠AOB=∠OBA
∴∠AOB=∠CEB
∴CE∥AO
∵EF⊥AO
∴EF⊥CE
∴EF是⊙C的切线
(3)作AH⊥OB于H,∴OH=HB=2,AH=4,AO=AB=![]()
∴sin∠AOB=sin∠ABO=![]()
在RT△EFO中,EF=OEsin∠BOA=![]()
由(2)CE∥OA,∴△BEC∽△BOA,
∴![]() ,即
,即![]()
∴BE=![]()
∴OE=OB﹣EB=![]()
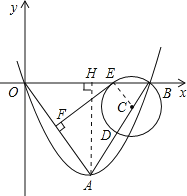
∴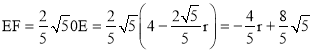
即:![]() ,
,
∴0<r<![]() .
.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:
【题目】如图,点P是菱形ABCD边上的一动点,它从点A出发沿着A→B→C→D路径匀速运动到点D,设△PAD的面积为y,P点的运动时间为x,则y关于x的函数图象大致为( )
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
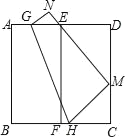
【题目】如图,将边长为3的正方形纸片ABCD对折,使AB与DC重合,折痕为EF,展平后,再将点B折到边CD上,使边AB经过点E,折痕为GH,点B的对应点为M,点A的对应点为N,那么折痕GH的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,弹性小球从点P(0,3)出发,沿所示方向运动,每当小球碰到矩形OABC的边时反弹,反弹时反射角等于入射角,当小球第1次碰到矩形的边时的点为P1,第2次碰到矩形的边时的点为P2,…,第n次碰到矩形的边时的点为Pn,则点P2的坐标是_____,点P2017的坐标是_____.
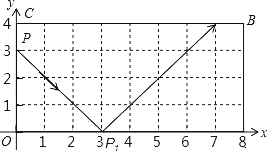
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△AOB和△COD均为等腰直角三角形,∠AOB=∠COD=90°,AO=4,CO=2,接连接AD,BC、点H为BC中点,连接OH.
(1)如图1所示,求证:OH=![]() AD且OH⊥AD;
AD且OH⊥AD;
(2)将△COD绕点O旋转到图2所示位置时,线段OH与AD又有怎样的关系,证明你的结论;
(3)请直接写出线段OH的取值范围.
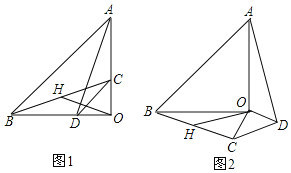
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是边长为10的菱形,对角线AC、BD相交于点E,过点C作CF∥DB交AB延长线于点F,联结EF交BC于点H.
(1)如图1,当EF⊥BC时,求AE的长;
(2)如图2,以EF为直径作⊙O,⊙O经过点C交边CD于点G(点C、G不重合),设AE的长为x,EH的长为y;
①求y关于x的函数关系式,并写出定义域;
②联结EG,当△DEG是以DG为腰的等腰三角形时,求AE的长.
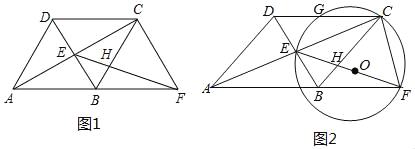
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的两边OA,OC分别在x轴和y轴上,并且OA=5,OC=3.若把矩形OABC绕着点O逆时针旋转,使点A恰好落在BC边上的A1处,则点C的对应点C1的坐标为( )
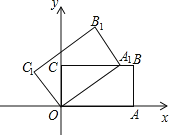
A. (﹣![]() ) B. (﹣
) B. (﹣![]() ) C. (﹣
) C. (﹣![]() ) D. (﹣
) D. (﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
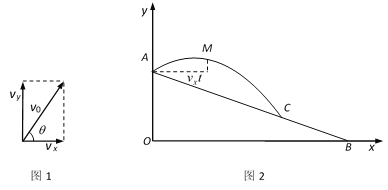
【题目】如图1,已知水龙头喷水的初始速度v0可以分解为横向初始速度vx和纵向初始速度vy,θ是水龙头的仰角,且![]() .图2是一个建在斜坡上的花圃场地的截面示意图,水龙头的喷射点A在山坡的坡顶上(喷射点离地面高度忽略不计),坡顶的铅直高度OA为15米,山坡的坡比为
.图2是一个建在斜坡上的花圃场地的截面示意图,水龙头的喷射点A在山坡的坡顶上(喷射点离地面高度忽略不计),坡顶的铅直高度OA为15米,山坡的坡比为![]() .离开水龙头后的水(看成点)获得初始速度v0米/秒后的运动路径可以看作是抛物线,点M是运动过程中的某一位置.忽略空气阻力,实验表明:M与A的高度之差d(米)与喷出时间t(秒)的关系为
.离开水龙头后的水(看成点)获得初始速度v0米/秒后的运动路径可以看作是抛物线,点M是运动过程中的某一位置.忽略空气阻力,实验表明:M与A的高度之差d(米)与喷出时间t(秒)的关系为![]() ;M与A的水平距离为
;M与A的水平距离为![]() 米.已知该水流的初始速度
米.已知该水流的初始速度![]() 为15米/秒,水龙头的仰角θ为
为15米/秒,水龙头的仰角θ为![]() .
.
(1)求水流的横向初始速度vx和纵向初始速度vy;
(2)用含t的代数式表示点M的横坐标x和纵坐标y,并求y与x的关系式(不写x的取值范围);
(3)水流在山坡上的落点C离喷射点A的水平距离是多少米?若要使水流恰好喷射到坡脚B处的小树,在相同仰角下,则需要把喷射点A沿坡面AB方向移动多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】美丽的黄河宛如一条玉带穿城而过,沿河两岸的滨河路风情线是兰州最美的景观之一.数学课外实践活动中,小林在南滨河路上的A,B两点处,利用测角仪分别对北岸的一观景亭D进行了测量.如图,测得∠DAC=45°,∠DBC=65°.若AB=132米,求观景亭D到南滨河路AC的距离(结果精确到1米,参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com