
【题目】为了丰富学生课余生活,某区教育部门准备在七年级开设兴趣课堂.为了了解学生对音乐、书法、球类、绘画这四个兴趣小组的喜爱情况,在全区进行随机抽样调查,并根据收集的数据绘制了下面两幅统计图(信息不完整),请根据图中提供的信息,解答下面的问题:

(1)此次共调查了多少名同学?
(2)将条形图补充完整,并计算扇形统计图中音乐部分的圆心角的度数
(3)如果该区七年级共有2000名学生参加这4个课外兴趣小组,而每名教师最多只能辅导本组的20名学生,则绘画兴趣小组至少需要准备多少名教师?
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠A=90°,CE⊥BD于E,AB=EC.
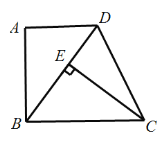
(1)求证:△ABD≌△ECB;
(2)若∠EDC=65°,求∠ECB的度数;
(3)若AD=3,AB=4,求DC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市正在开展“食品安全城市”创建活动,为了解学生对食品安全知识的了解情况,学校随机抽取了部分学生进行问卷调查,将调查结果按照“A非常了解、B了解、C了解较少、D不了解”四类分别进行统计,并绘制了下列两幅统计图(不完整).请根据图中信息,解答下列问题:

(1)此次共调查了 名学生;
(2)扇形统计图中D所在扇形的圆心角为 ;
(3)将上面的条形统计图补充完整;
(4)若该校共有800名学生,请你估计对食品安全知识“非常了解”的学生的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A(α,0)、B(b,0),点C在y轴上,且由|a+4|+(b-2)2=0.
(1)若S△ABC=6,求C点的坐标;
(2)将C向右平移,使OC平分∠ACB,点P是x轴上B点右边的一动点,PQ⊥OC于Q点.当∠ABC-∠BAC=60°时,求∠APQ的度数;
(3)在(2)的条件下,将线段AC平移,使其经过P点得线段EF,作∠APE的角平分线交OC的延长线于点M.当P点在x轴上运动时,求∠M-![]() ∠ABC的值.
∠ABC的值.

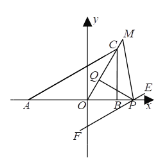
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甘肃省省府兰州,又名金城,在金城,黄河母亲河通过自身文化的演绎,衍生和流传了独特的“金城八宝”美食,“金城八宝”美食中甜品类有:味甜汤糊“灰豆子”、醇香软糯“甜胚子”、生津润肺“热冬果”、香甜什锦“八宝百合”;其他类有:青白红绿“牛肉面”、酸辣清凉“酿皮子”、清爽溜滑“浆水面”、香醇肥美“手抓羊肉”,李华和王涛同时去品尝美食,李华准备在“甜胚子、牛肉面、酿皮子、手抓羊肉”这四种美食中选择一种,王涛准备在“八宝百合、灰豆子、热冬果、浆水面”这四种美食中选择一种。(甜胚子、牛肉面、酿皮子、手抓羊肉分别记为A、B、C、D;八宝百合、灰豆子、热冬果、浆水面分别记为E、F、G、H)
(1)用树状图或表格的方法表示李华和王涛同时选择美食的所有可能结果;
(2)求李华和王涛同时选择的美食都是甜品类的概率。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组开展了一次活动,过程如下:设∠BAC=θ(0°<θ<90°).现把小棒依次摆放在两射线之间,并使小棒两端分别落在射线AB、AC上.
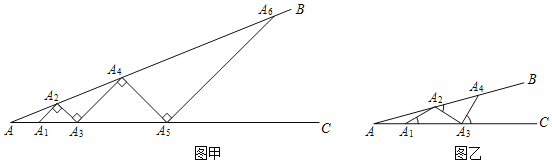
活动一:如图甲所示,从点A1开始,依次向右摆放小棒,使小棒与小棒在端点处互相垂直.(A1A2为第1根小棒)
数学思考:
(1)小棒能无限摆下去吗?答: .(填“能”或“不能”)
(2)设AA1=A1A2=A2A3,求θ的度数;
活动二:如图乙所示,从点A1开始,用等长的小棒依次向右摆放,其中A1A2为第一根小棒,且A1A2=AA1.
数学思考:
(3)若已经摆放了3根小棒,则θ1= ,θ2= ,θ3= ;(用含θ的式子表示)
(4)若只能摆放5根小棒,求θ的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△PQR是△ABC经过某种变换后得到的图形,其中点A与点P,点B与点Q,点C与点R是对应的点,在这种变换下:
(1)直接写出下列各点的坐标
①A(____,_____)与P(_____,_____);B(_____,_____)与Q(______,_____);C(_____,______)与R(______,______)
②它们之间的关系是:______(用文字语言直接写出)
(2)在这个坐标系中,三角形ABC内有一点M,点M经过这种变换后得到点N,点N在三角形PQR内,其中M、N的坐标M(![]() ,6(a+b)﹣10),N(1﹣
,6(a+b)﹣10),N(1﹣![]() ,4(b﹣2a)﹣6),求关于x的不等式
,4(b﹣2a)﹣6),求关于x的不等式![]() ﹣
﹣![]() >b﹣1的解集.
>b﹣1的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,分别过B,C向经过点A的直线EF作垂线,垂足为E,F.
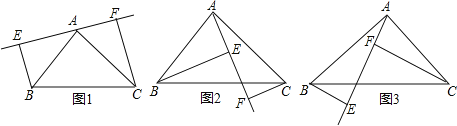
(1)如图1,当EF与斜边BC不相交时,请证明EF=BE+CF;
(2)如图2,当EF与斜边BC相交时,其他条件不变,写出EF、BE、CF之间的数量关系,并说明理由;
(3)如图3,猜想EF、BE、CF之间又存在怎样的数量关系,写出猜想,不必说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中装有大小和形状相同的3个红球和2个白球,把它们充分搅匀.
(1)“从中任意抽取1个球不是红球就是白球”是 事件,“从中任意抽取1个球是黑球”是 事件;
(2)从中任意抽取1个球恰好是红球的概率是 ;
(3)学校决定在甲、乙两名同学中选取一名作为学生代表发言,制定如下规则:从盒子中任取两个球,若两球同色,则选甲;若两球异色,则选乙.你认为这个规则公平吗?请用列表法或画树状图法加以说明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com