
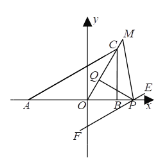
【题目】已知A(α,0)、B(b,0),点C在y轴上,且由|a+4|+(b-2)2=0.
(1)若S△ABC=6,求C点的坐标;
(2)将C向右平移,使OC平分∠ACB,点P是x轴上B点右边的一动点,PQ⊥OC于Q点.当∠ABC-∠BAC=60°时,求∠APQ的度数;
(3)在(2)的条件下,将线段AC平移,使其经过P点得线段EF,作∠APE的角平分线交OC的延长线于点M.当P点在x轴上运动时,求∠M-![]() ∠ABC的值.
∠ABC的值.

【答案】(1) C(0,2)或(0,-2);(2)∠APQ=30°;(3)∠M-![]() ∠ABC=0.
∠ABC=0.
【解析】
(1)根据已知条件求出点A,B的坐标,结合三角形的面积公式求出点C的纵坐标,即可求出点C的坐标.
(2)根据∠COB为![]() AOC的外角可得∠COB=∠BAC+
AOC的外角可得∠COB=∠BAC+![]() ∠ACB,后根据三角形内角和定理可用∠ABC和∠ACB表示∠COB,结合两式及∠ABC-∠BAC=60°即可求解.
∠ACB,后根据三角形内角和定理可用∠ABC和∠ACB表示∠COB,结合两式及∠ABC-∠BAC=60°即可求解.
(3)根据三角形内角和定理结合题(1)可得∠M+∠MPO=120°,后根据EF∥AC,∠BAC=∠APF以及PM平分∠OPE可得∠MPO=90°-![]() ∠BAC,再根据已知条件∠ABC-∠BAC=60°,结合三式即可求得∠M-
∠BAC,再根据已知条件∠ABC-∠BAC=60°,结合三式即可求得∠M-![]() ∠ABC的值.
∠ABC的值.
解:(1) 由已知条件 |a+4|+(b-2)2=0
可求得a=-4,b=2,即A(-4,0)、B(2,0)
S△ABC=![]() (|a|+b)c=6
(|a|+b)c=6
可求得c=2
即点C坐标为(0,2)或(0,-2).
(2) ∵∠COB=∠BAC+![]() ∠ACB;
∠ACB;
又∵∠COB=180°-∠ABC-![]() ∠ACB
∠ACB
∴2∠COB=180°+∠BAC-∠ABC,∠ABC-∠BAC=60°
∴∠COB=60°,∴∠APQ=30°
(3) 在△OMP中,∠M+∠MOP+∠MPO=180°,∠M+∠MPO=120°
∵EF∥AC,∴∠BAC=∠APF,
∴∠MPO=![]() (180°-∠APF )=90°-
(180°-∠APF )=90°-![]() ∠BAC,∠BAC=∠ABC-60°
∠BAC,∠BAC=∠ABC-60°
∴∠MPO=120°-![]() ∠ABC
∠ABC
∴∠M+120°-![]() ∠ABC=120°,∴∠M-
∠ABC=120°,∴∠M-![]() ∠ABC=0
∠ABC=0


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】课外阅读是提高学生素养的重要途径,某校为了了解学生课外阅读情况,随机抽查了50名学生,统计他们平均每天课外阅读时间(t小时),根据t的长短分为A,B,C,D四类.下面是根据所抽查的人数绘制的两幅不完整的统计图表,请根据图中提供的信息,解答下面的问题:

(1)求表格中的a值,并在图中补全条形统计图;
(2)该校现有1300名学生,请你估计该校共有多少学生课外阅读时间不少于1小时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明:
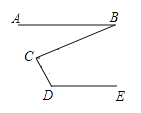
已知:如图,AB∥DE,求证:∠D+∠BCD﹣∠B=180°,
证明:过点C作CF∥AB.
∵AB∥CF(已知),
∴∠B= ( ).
∵AB∥DE,CF∥AB( 已知 ),
∴CF∥DE ( )
∴∠2+ =180° ( )
∵∠2=∠BCD﹣∠1,
∴∠D+∠BCD﹣∠B=180° ( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的文字,解答问题:
大家知道![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此![]() 的小数部分我们不可能全部地写出来,于是小明用
的小数部分我们不可能全部地写出来,于是小明用![]() -1来表示
-1来表示![]() 的小数部分,你同意小明的表示方法吗?
的小数部分,你同意小明的表示方法吗?
事实上,小明的表示方法是有道理,因为![]() 的整数部分是1,将这个数减去其整数部分,差就是小数部分.
的整数部分是1,将这个数减去其整数部分,差就是小数部分.
又例如:∵![]() ,即
,即![]() ,
,
∴![]() 的整数部分为2,小数部分为(
的整数部分为2,小数部分为(![]() -2).
-2).
请解答:(1) ![]() 的整数部分是 ,小数部分是 .
的整数部分是 ,小数部分是 .
(2)如果![]() 的小数部分为a,
的小数部分为a, ![]() 的整数部分为b,求a+b-
的整数部分为b,求a+b-![]() 的值;
的值;
(3)已知: 10+![]() =x+y,其中x是整数,且0<y<1,求x-y的相反数.
=x+y,其中x是整数,且0<y<1,求x-y的相反数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中每个小正方形边长都是1.
(1)画出△ABC关于直线1对称的图形△A1BlCl;
(2)在直线l上找一点P,使PB=PC;(要求在直线1上标出点P的位置)
(3)连接PA、PC,计算四边形PABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,有一正方形广场ABCD,图形中的线段均表示直行道路,![]() 表示一条以A为圆心,以AB为半径的圆弧形道路.如图2,在该广场的A处有一路灯,O是灯泡,夜晚小齐同学沿广场道路散步时,影子长度随行走路线的变化而变化,设他步行的路程为x (m)时,相应影子的长度为y (m),根据他步行的路线得到y与x之间关系的大致图象如图3,则他行走的路线是( )
表示一条以A为圆心,以AB为半径的圆弧形道路.如图2,在该广场的A处有一路灯,O是灯泡,夜晚小齐同学沿广场道路散步时,影子长度随行走路线的变化而变化,设他步行的路程为x (m)时,相应影子的长度为y (m),根据他步行的路线得到y与x之间关系的大致图象如图3,则他行走的路线是( )

A. A→B→E→G B. A→E→D→C C. A→E→B→F D. A→B→D→C
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富学生课余生活,某区教育部门准备在七年级开设兴趣课堂.为了了解学生对音乐、书法、球类、绘画这四个兴趣小组的喜爱情况,在全区进行随机抽样调查,并根据收集的数据绘制了下面两幅统计图(信息不完整),请根据图中提供的信息,解答下面的问题:

(1)此次共调查了多少名同学?
(2)将条形图补充完整,并计算扇形统计图中音乐部分的圆心角的度数
(3)如果该区七年级共有2000名学生参加这4个课外兴趣小组,而每名教师最多只能辅导本组的20名学生,则绘画兴趣小组至少需要准备多少名教师?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,AD⊥BC于点D,CE⊥AB于点E.

(1)猜测∠1与∠2的关系,并说明理由;
(2)如果∠ABC是钝角,如图2,(1)中的结论是否还成立?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=8,BC=6,点D为AC边上的动点,点D从点C出发,沿边CA向点A运动,当运动到点A时停止,若设点D运动的时间为t秒.点D运动的速度为每秒1个单位长度.

(1)当t=2时,CD= , AD= ;
(2)求当t为何值时,△CBD是直角三角形,说明理由;
(3)求当t为何值时,△CBD是以BD或CD为底的等腰三角形?并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com