
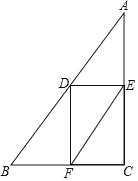
【题目】如图,在△ABC中,∠C=90°,点D是边AB上的动点,过点D作DE∥BC交AC于E,过E作EF∥AB交BC于F,连结DF.
(1)若点D是AB的中点,证明:四边形DFEA是平行四边形;
(2)若AC=8,BC=6,直接写出当△DEF为直角三角形时AD的长.
【答案】(1)见解析;(2)AD的值为5或![]() .
.
【解析】
(1)先证明DF∥AE,EF∥AD即可;
(2)分两种情形分别求解即可解决问题;
(1)证明:∵AD=DB,DE∥BC,
∴AE=EC,
∵EF∥AB,
∴BF=CF,∵AD=DB,
∴DF∥AC,∵EF∥AB,
∴四边形DFEA是平行四边形.
(2)情形1:当点D是AB的中点,由(1)可知:DE∥BC,DF∥EC,
∴四边形DECF是平行四边形,
∵∠ECF=90°,
∴四边形DECF是矩形,
∴∠EDF=90°,△DEF是直角三角形,此时AD=![]() AB=
AB=![]() ×
×![]() =5.
=5.
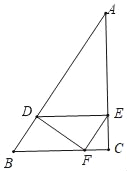
情形2:如图,当∠DFE=90°时,设AD=x.
则AE=![]() x.BD=10﹣x,EC=8﹣
x.BD=10﹣x,EC=8﹣![]() x,BF=
x,BF=![]() (10﹣x),CF=
(10﹣x),CF=![]() (8﹣
(8﹣![]() x),
x),
∵BF+CF=6,
∴![]() (10﹣x)+
(10﹣x)+![]() (8﹣
(8﹣![]() x)=6
x)=6
∴x=![]() ,
,
综上所述,AD的值为5或![]() .
.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:
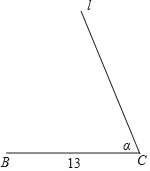
【题目】如图,线段BC长为13,以C为顶点,CB为一边的∠α满足cosα=![]() .锐角△ABC的顶点A落在∠α的另一边上,且满足sinA=
.锐角△ABC的顶点A落在∠α的另一边上,且满足sinA=![]() .求△ABC的高BD及AB边的长,并结合你的计算过程画出高BD及AB边.(图中提供的单位长度供补全图形使用)
.求△ABC的高BD及AB边的长,并结合你的计算过程画出高BD及AB边.(图中提供的单位长度供补全图形使用)
查看答案和解析>>
科目:初中数学 来源: 题型:
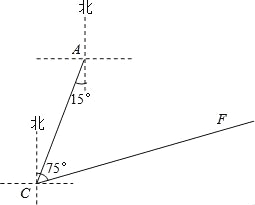
【题目】中考英语听力测试期间T需要杜绝考点周围的噪音.如图,点A是某市一中考考点,在位于考点南偏西15°方向距离500米的C点处有一消防队.在听力考试期间,消防队突然接到报警电话,消防车需沿北偏东75°方向的公路CF前往救援.已知消防车的警报声传播半径为400米,若消防车的警报声对听力测试造成影响,则消防车必须改道行驶.试问:消防车是否需要改道行驶?
说明理由.(![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直线l:y=3x+3与x轴交于点A,与y轴交于点B.把△AOB沿y轴翻折,点A落到点C,抛物线过点B、C和D(3,0).
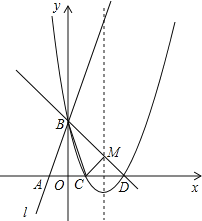
(1)求直线BD和抛物线的解析式.
(2)若BD与抛物线的对称轴交于点M,点N在坐标轴上,以点N、B、D为顶点的三角形与△MCD相似,求所有满足条件的点N的坐标.
(3)在抛物线上是否存在点P,使S△PBD=6?若存在,求出点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
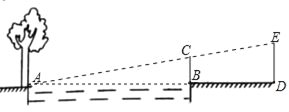
【题目】如图,洋洋和华华用所学的数学知识测量一条小河的宽度,河的对岸有一棵大树,底部记为点A,在他们所在的岸边选择了点B,并且使AB与河岸垂直,在B处与地面垂直竖起标杆BC,再在AB的延长线上选择点D,与地面垂直竖起标杆DE,使得A、C、E三点共线.经测量,BC=1m,DE=1.5m,BD=5m,求小河的宽度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,∠ADC的平分线与AB交于E,点F在DE的延长线上,∠BFE=90°,连接AF、CF,CF与AB交于G.有以下结论:
①AE=BC
②AF=CF
③BF2=FGFC
④EGAE=BGAB
其中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
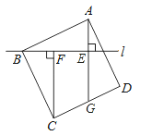
【题目】如图,过正方形ABCD的顶点B作直线l,过点A,C作直线l的垂线,垂足分别为E,F,直线AE交CD于点G.
(1)求证:△ABE≌△BCF;
(2)若∠CBF=65°,求∠AGC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
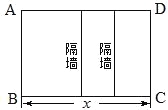
【题目】某工厂拟建一座平面图形为矩形且面积为200平方米的三级污水处理池(平面图如图ABCD所示).由于地形限制,三级污水处理池的长、宽都不能超过16米.如果池的外围墙建造单价为每米400元,中间两条隔墙建造单价为每米300元,池底建造单价为每平方米80元.(池墙的厚度忽略不计)当三级污水处理池的总造价为47200元时,求池长x.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,以点B为圆心,BC长为半径画弧,交线段AB于点D;以点A为圆心,AD长为半径画弧,交线段AC于点E,连结CD.

(1)若∠A=28°,求∠ACD的度数.
(2)设BC=a,AC=b.
①线段AD的长是方程x2+2ax﹣b2=0的一个根吗?说明理由.
②若AD=EC,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com