
【题目】如图,在△ABC中,∠ACB=90°,以点B为圆心,BC长为半径画弧,交线段AB于点D;以点A为圆心,AD长为半径画弧,交线段AC于点E,连结CD.

(1)若∠A=28°,求∠ACD的度数.
(2)设BC=a,AC=b.
①线段AD的长是方程x2+2ax﹣b2=0的一个根吗?说明理由.
②若AD=EC,求![]() 的值.
的值.
【答案】(1)31°;(2)①是,理由见解析;②![]()
【解析】
(1)根据三角形内角和定理求出∠B,根据等腰三角形的性质求出∠BCD,计算即可;
(2)①根据勾股定理求出AD,利用求根公式解方程,比较即可;
②根据勾股定理列出算式,计算即可.
解:(1)∵∠ACB=90°,∠A=28°,
∴∠B=62°,
∵BD=BC,
∴∠BCD=∠BDC=59°,
∴∠ACD=90°﹣∠BCD=31°;
(2)①由勾股定理得,AB=![]() =
=![]() ,
,
∴AD=![]() ﹣a,
﹣a,
解方程x2+2ax﹣b2=0得,x=![]() =
=![]() ﹣a,
﹣a,
∴线段AD的长是方程x2+2ax﹣b2=0的一个根;
②∵AD=AE,
∴AE=EC=![]() ,
,
由勾股定理得,a2+b2=(![]() b+a)2,
b+a)2,
整理得,![]() .
.


科目:初中数学 来源: 题型:
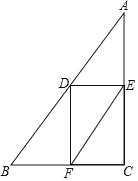
【题目】如图,在△ABC中,∠C=90°,点D是边AB上的动点,过点D作DE∥BC交AC于E,过E作EF∥AB交BC于F,连结DF.
(1)若点D是AB的中点,证明:四边形DFEA是平行四边形;
(2)若AC=8,BC=6,直接写出当△DEF为直角三角形时AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究
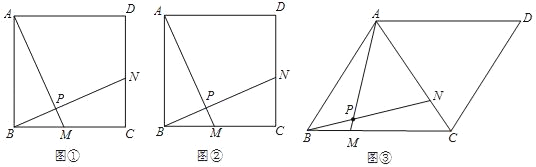
(1)如图①,已知正方形ABCD的边长为4.点M和N分别是边BC、CD上两点,且BM=CN,连接AM和BN,交于点P.猜想AM与BN的位置关系,并证明你的结论.
(2)如图②,已知正方形ABCD的边长为4.点M和N分别从点B、C同时出发,以相同的速度沿BC、CD方向向终点C和D运动.连接AM和BN,交于点P,求△APB周长的最大值;
问题解决
(3)如图③,AC为边长为2![]() 的菱形ABCD的对角线,∠ABC=60°.点M和N分别从点B、C同时出发,以相同的速度沿BC、CA向终点C和A运动.连接AM和BN,交于点P.求△APB周长的最大值.
的菱形ABCD的对角线,∠ABC=60°.点M和N分别从点B、C同时出发,以相同的速度沿BC、CA向终点C和A运动.连接AM和BN,交于点P.求△APB周长的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连接CE.

(1)求证:BD=EC;
(2)若∠E=50°,求∠BAO的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
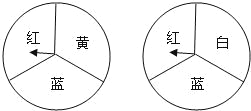
【题目】小明和小刚用如图所示的两个转盘做配紫色游戏,游戏规则是:分别旋转两个转盘,若其中一个转盘转出了红色,另一个转出了蓝色则可以配成紫色.此时小刚得1分,否则小明得1分.这个游戏规则对双方公平吗?请说明理由.若你认为不公平,如何修改规则才能使游戏对双方公平?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A. 为检测我市正在销售的酸奶质量,应该采用普查的方式
B. 若两名同学连续五次数学测试的平均分相同,则方差较大的同学数学成绩更稳定
C. 抛掷一个正方体骰子,朝上的面的点数为奇数的概率是![]()
D. “打开电视,正在播放广告”是必然事件
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级一班数学调研考试成绩绘制成频数分布直方图,如图(得分取整数).请根据所给信息解答下列问题:
(1)这个班有多少人参加了本次数学调研考试?
(2)60.5~70.5分数段的频数和频率各是多少?
(3)请你根据统计图,提出一个与(1),(2)不同的问题,并给出解答.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形纸片BDEF和直角三角板BCA,点A在EF上,AC=DE=![]() ,FE=3
,FE=3![]() ,∠C=90°,∠CBA=30°.
,∠C=90°,∠CBA=30°.
(1)写出三种不同类型的结论.
(2)将直角三角板绕点B旋转,在旋转过程中,
①求点A与点E的最短距离;
②若将直角三角板绕点B从①中位置开始顺时针旋转α度(0≤α≤360),使∠BAE=90°,求α的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com