
【题目】用黑白棋子摆出下列一组图形,根据规律可知.
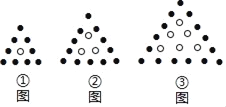
(1)在第n个图中,白棋共有 枚,黑棋共有 枚;
(2)在第几个图形中,白棋共有300枚;
(3)白棋的个数能否与黑棋的个数相等?若能,求出是第几个图形,若不能,说明理由.
【答案】(1)![]() n(n+1),3n+6;(2)第24个图形中,白棋共有300枚;(3)白棋的个数不能与黑棋的个数相等.
n(n+1),3n+6;(2)第24个图形中,白棋共有300枚;(3)白棋的个数不能与黑棋的个数相等.
【解析】
(1)观察图形可得:第一个图形有白棋1=![]() 枚,黑棋9=3×1+6枚;第二个图形有白棋3=
枚,黑棋9=3×1+6枚;第二个图形有白棋3=![]() 枚,黑棋12=3×2+6枚;第三个图形有白棋6=
枚,黑棋12=3×2+6枚;第三个图形有白棋6=![]() 枚,黑棋15=3×3+6枚;…由此可得,第n个图中,白棋共有
枚,黑棋15=3×3+6枚;…由此可得,第n个图中,白棋共有![]() 枚,黑棋共有3n+6枚;(2)令
枚,黑棋共有3n+6枚;(2)令![]() =300,解方程求得n的值即可;(3)令
=300,解方程求得n的值即可;(3)令![]() =3n+6,解方程求得n的值,若n为正整数,则白棋的个数能与黑棋的个数相等,否则,不能.
=3n+6,解方程求得n的值,若n为正整数,则白棋的个数能与黑棋的个数相等,否则,不能.
解:(1)由题意得:白棋为:![]() n(n+1),黑棋为3n+6;
n(n+1),黑棋为3n+6;
故答案为:![]() n(n+1),3n+6;
n(n+1),3n+6;
(2)![]() n(n+1)=300,解得:n=24(已舍去负值)
n(n+1)=300,解得:n=24(已舍去负值)
故:第24个图形中,白棋共有300枚;
(3)![]() n(n+1)=3n+6;
n(n+1)=3n+6;
解得:n=![]() 为无理数,不是整数,
为无理数,不是整数,
∴白棋的个数不能与黑棋的个数相等.


科目:初中数学 来源: 题型:
【题目】(6分)现有5个质地、大小完全相同的小球上分别标有数字﹣1,﹣2,1,2,3.先将标有数字﹣2,1,3的小球放在第一个不透明的盒子里,再将其余小球放在第二个不透明的盒子里.现分别从两个盒子里各随即取出一个小球.
(1)请利用列表或画树状图的方法表示取出的两个小球上数字之和所有可能的结果;
(2)求取出的两个小球上的数字之和等于0的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+2ax+3a2+3(其中x是自变量),当x≥2时,y随x的增大而增大,且2≤x≤1时,y的最大值为9,则a的值为
A. 1或2 B. ![]() 或
或![]()
C. ![]() D. 1
D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AC=2AB,将矩形ABCD绕点A旋转得到矩形AB′C′D′,使点B的对应点B'落在AC上,B'C'交AD于点E,在B'C′上取点F,使B'F=AB.
(1)求证:AE=C′E.
(2)求∠FBB'的度数.
(3)已知AB=2,求BF的长.
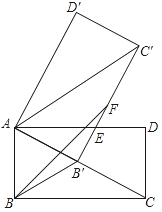
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小张准备把一根长为32cm的铁丝剪成两段,并把每一段各围成一个正方形.(1)要使这两个正方形的面积之和等于40cm2,小张该怎么剪?
(2)小李对小张说:“这两个正方形的面积之和不可能等于30cm2.”他的说法对吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,禁渔期间,我渔政船在A处发现正北方向B处有一艘可疑船只,测得A、B两处距离为99海里,可疑船只正沿南偏东53°方向航行.我渔政船迅速沿北偏东27°方向前去拦截,2小时后刚好在C处将可疑船只拦截.求该可疑船只航行的速度.
(参考数据:sin27°≈![]() , cos27°≈
, cos27°≈![]() , tan27°≈
, tan27°≈![]() , sin53°≈
, sin53°≈![]() , cos53°≈
, cos53°≈![]() , tan53°≈
, tan53°≈![]() )
)
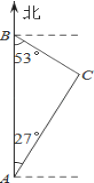
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:抛物线y=-![]() +bx+c经过A(-1,0)、B(5,0)两点,顶点为P.
+bx+c经过A(-1,0)、B(5,0)两点,顶点为P.
求:(1)求b,c的值;
(2)求△ABP的面积;
(3)若点C(![]() ,
,![]() )和点D(
)和点D(![]() ,
,![]() )在该抛物线上,则当
)在该抛物线上,则当![]() 时,请写出
时,请写出![]() 与
与![]() 的大小关系.
的大小关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(感知)如图①,在四边形ABCD中,点P在边AB上(点P不与点A、B重合),∠A=∠B=∠DPC=90°.易证:△DAP∽△PBC(不要求证明).
(探究)如图②,在四边形ABCD中,点P在边AB上(点P不与点A、B重合),∠A=∠B=∠DPC.
(1)求证:△DAP~△PBC.
(2)若PD=5,PC=10,BC=9,求AP的长.
(应用)如图③,在△ABC中,AC=BC=4,AB=6,点P在边AB上(点P不与点A、B重合),连结CP,作∠CPE=∠A,PE与边BC交于点E.当CE=3EB时,求AP的长.
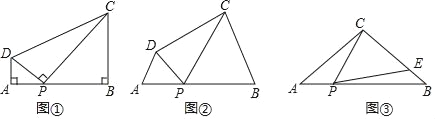
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com