
 ��ͼ����ֱ֪��l1��y=x+3��x�ύ�ڵ�A����y�ύ�ڵ�B����ֱ��l2��y=-$\frac{1}{2}$x���ڵ�P��ֱ��l3��y=-$\frac{3}{2}$x+4��x�ύ�ڵ�C����y�ύ�ڵ�D����ֱ��l1���ڵ�Q����ֱ��l2���ڵ�R��
��ͼ����ֱ֪��l1��y=x+3��x�ύ�ڵ�A����y�ύ�ڵ�B����ֱ��l2��y=-$\frac{1}{2}$x���ڵ�P��ֱ��l3��y=-$\frac{3}{2}$x+4��x�ύ�ڵ�C����y�ύ�ڵ�D����ֱ��l1���ڵ�Q����ֱ��l2���ڵ�R������ ��1��ֱ��l1��y=x+3��x�ύ�ڵ�A����y�ύ�ڵ�B����y=0�����x=-3����x=0�����y=3���õ�A��B�����꽫ֱ��l1��y=x+3��ֱ��l2��y=-$\frac{1}{2}$x��������й�x��y�ķ����飬�ⷽ�̾��������ֱ�ߵĽ���P���ꣻ
��2�����P������꣬����y=-$\frac{3}{2}$x+4�����жϣ�
��3�����Q��R��C������꣬Ȼ����ݼ�����ã�
��� �⣺��1����ֱ��l1��y=x+3��x�ύ�ڵ�A����y�ύ�ڵ�B��
����y=0�����x=-3����x=0�����y=3��
��A��-3��0����B��0��3����
��ֱ��l1��ֱ��l2y=-$\frac{1}{2}$x���ڵ�P��
���$\left\{\begin{array}{l}{y=x+3}\\{y=-\frac{1}{2}x}\end{array}\right.$��$\left\{\begin{array}{l}{x=-2}\\{y=1}\end{array}\right.$��
��P��-2��1����
�ʴ�Ϊ����-3��0������0��3������-2��1����
��2����P?��ֱ��l3��
��P��-2��1�����ҽ���POB��y���۵���P?���P����y��Գƣ�
��P?��2��1����
��x=2ʱ������y=-$\frac{3}{2}$x+4��y=-$\frac{3}{2}$��2+4=1��
���P?��ֱ��l3�ϣ�
��3���ֱ����P��PE��x����F������Q��QF��x����F������R��RG��x����G��
��$\left\{\begin{array}{l}{y=x+3}\\{y=-\frac{3}{2}x+4}\end{array}\right.$ ��$\left\{\begin{array}{l}{x=\frac{2}{5}}\\{y=\frac{17}{5}}\end{array}\right.$��
��Q��$\frac{2}{5}$��$\frac{17}{5}$����
��$\left\{\begin{array}{l}{y=-\frac{1}{2}x}\\{y=-\frac{3}{2}x+4}\end{array}\right.$ ��$\left\{\begin{array}{l}{x=4}\\{y=-2}\end{array}\right.$
��R��4��-2����
����y=-$\frac{3}{2}$x+4����y=0��x=$\frac{8}{3}$��
��C��$\frac{8}{3}$��0����
��S��AQC=$\frac{1}{2}$AC��QF=$\frac{1}{2}$����$\frac{8}{3}$+3����$\frac{17}{5}$=$\frac{289}{30}$��S��OCR=$\frac{1}{2}$OC•GR=$\frac{1}{2}$��$\frac{8}{3}$��2=$\frac{8}{3}$��S��AOP=$\frac{1}{2}$OA•PE=$\frac{1}{2}$��3��1=$\frac{3}{2}$��
��S��PQR=S��AQC+S��OCR-S��AOP=$\frac{289}{30}$+$\frac{8}{3}$-$\frac{3}{2}$=$\frac{54}{5}$��
���� ���⿼��������ֱ���ཻ��ƽ�����⣺����ֱ�ߵĽ������꣬������������ֱ�����Ӧ��һ�κ�������ʽ����ɵĶ�Ԫһ�η�����Ľ⣻������ֱ����ƽ�еĹ�ϵ����ô���ǵ��Ա���ϵ����ͬ����kֵ��ͬ�����磺��ֱ��y1=k1x+b1��ֱ��y2=k2x+b2ƽ�У���ôk1=k2��


 Сѧ���AB��ϵ�д�
Сѧ���AB��ϵ�д� ABC����ȫ�ž�ϵ�д�
ABC����ȫ�ž�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
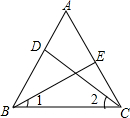 ��ͼ���ڵȱߡ�ABC�У�DE�ֱ���AB��AC�ϵĵ㣬��AD=CE��
��ͼ���ڵȱߡ�ABC�У�DE�ֱ���AB��AC�ϵĵ㣬��AD=CE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ֱ������ϵxOy�У�ֱ��l���㣨0��1������x��ƽ�У���ABC����ֱ��l�Գƣ���֪��A�����ǣ�4��4�������B�������ǣ�4��-2����
��ͼ����ֱ������ϵxOy�У�ֱ��l���㣨0��1������x��ƽ�У���ABC����ֱ��l�Գƣ���֪��A�����ǣ�4��4�������B�������ǣ�4��-2�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��֪��a��b�������ϱ�ʾ�ĵ��λ����ͼ��ʾ�������н�����ȷ���ǣ�������
��֪��a��b�������ϱ�ʾ�ĵ��λ����ͼ��ʾ�������н�����ȷ���ǣ�������| A�� | a+b��0 | B�� | a•b��0 | C�� | |a|��|b| | D�� | b+a��b |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com