
【题目】如图,已知正方形ABCD的边长为3,E是对角线BD上一点(BE>DE).
(1)利用直尺和圆规,在图中过点E作AE的垂线,交BC边于点F(保留作图痕迹,不写作法);
(2)在(1)中,求证:AE=EF;
(3)若(1)中四边形ABFE的面积为4,求AE的长.

【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)过点E作AE的垂线即可;
(2)如图,过点E作EM⊥AB、EN⊥BC,先证明矩形MBNE是正方形,则∠AEM=∠FEN,再证明△AEM≌△FEN,从而得到AE=EF;
(3)利用△AEM≌△FEN得到S△AEM=S△FEN,则S四边形ABFE=S正方形MBNE,利用正方形面积公式得到BM=2,则AM=AB﹣BM=1,然后利用勾股定理计算AE的长.
(1)如图,
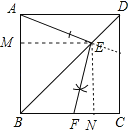
(2)如图,过点E作EM⊥AB、EN⊥BC,
∴∠EMB=∠MBN=∠ENB=90°,
∴四边形MBNE是矩形,
又∵四边形ABCD为正方形,
∴BD平分∠ABC,∴EM=EN,
∴矩形MBNE是正方形,
∵∠AEM+∠MEF=∠MEF+∠FEN=90°,
∴∠AEM=∠FEN,
又∵∠AME=∠FNE=90°,EM=EN,
∴△AEM≌△FEN(ASA),
∴AE=EF;
(3)∵△AEM≌△FEN,
∴S△AEM=S△FEN,
∴S四边形ABFE=S正方形MBNE,
∵四边形ABFE的面积为4,
∴BM2=4,
∴BM=2(取正舍负),
∴AM=AB﹣BM=1,
∴AE=![]()


科目:初中数学 来源: 题型:
【题目】某校为了解高一年级住校生在校期间的月生活支出情况,从高一年级600名住校学生中随机抽取部分学生,对他们今年4月份的生活支出情况进行调查统计,并绘制成如下统计图表:
组别 | 月生活支出x(单位:元) | 频数(人数) | 频率 |
第一组 | x<300 | 4 | 0.10 |
第二组 | 300≤x<350 | 2 | 0.05 |
第三组 | 350≤x<400 | 16 | n |
第四组 | 400≤x<450 | m | 0.30 |
第五组 | 450≤x<500 | 4 | 0.10 |
第六组 | x≥500 | 2 | 0.05 |
请根据图表中所给的信息,解答下列问题:
(1)在这次调查中共随机抽取了 名学生,图表中的m= ,n ;
(2)请估计该校高一年级600名住校学生今年4月份生活支出低于350元的学生人数;
(3)现有一些爱心人士有意愿资助该校家庭困难的学生,学校在本次调查的基础上,经过进一步核实,确认高一(2)班有A,B,C三名学生家庭困难,其中A,B为女生,C为男生.李阿姨申请资助他们中的两名,于是学校让李阿姨从A,B,C三名学生中依次随机抽取两名学生进行资助,请用列表法(或树状图法)求恰好抽到A,B两名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是_____.
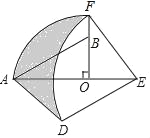
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,BE平分∠ABC,D是边AB上一点,以BD为直径的⊙O经过点E,且交BC于点F.
(1)求证:AC是⊙O的切线;
(2)若BF=12,⊙O的半径为10,求CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市中小学学生素养提升五项工程自启动以来,越来越受到教师、家长和学生的喜爱.为进一步了解学生对“规范书写”、“深度阅读”、“课堂演讲”、“阳光体艺”、“实验实践”的喜爱程度,某学生总数是1800人的九年一贯制学校,从每个年级随机抽取了部分学生进行了调查(每位学生只可选其中一项),并将结果整理、绘制成统计图如下:
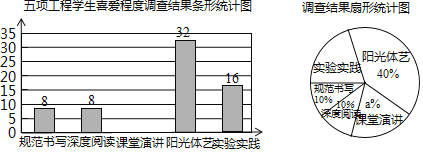
根据以上统计图,解答下列问题:
(1)本次接受调查的学生共有 人,补全条形统计图;
(2)求扇形统计图中a的值;
(3)估计该校全体学生中喜爱“实验实践”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四张大小、形状都相同的卡片上分别写有数字1,2,3,4,把它们放入到不透明的盒子中摇匀.
(1)从中随机抽出1张卡片,求抽出的卡片上的数字恰好是偶数的概率;
(2)从中随机抽出2张卡片,求抽出的2张卡片上的数字恰好是相邻两整数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列四个结论:①abc>0;3b+2c<0;③4a+c<2b;④当y>0时,﹣![]() <x<
<x<![]() .其中结论正确的个数是( )
.其中结论正确的个数是( )
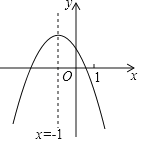
A. 2B. 3C. 4D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现如今,“垃圾分类”意识已深入人心,垃圾一般可分为:可回收物、厨余垃圾、有害垃圾、其它垃圾.其中甲拿了一袋垃圾,乙拿了两袋垃圾.
(1)直接写出甲所拿的垃圾恰好是“厨余垃圾”的概率;
(2)求乙所拿的两袋垃圾不同类的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com