
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+ ![]() 与x轴交于A(-3,0),B(1,0)两点,与y轴交于点C,点D与点C关于抛物线的对称轴对称.
与x轴交于A(-3,0),B(1,0)两点,与y轴交于点C,点D与点C关于抛物线的对称轴对称.
(1)求抛物线的解析式,并直接写出点D的坐标;
(2)如图1,点P从点A出发,以每秒1个单位长度的速度沿A→B匀速运动,到达点B时停止运动.以AP为边作等边△APQ(点Q在x轴上方).设点P在运动过程中,△APQ与四边形AOCD重叠部分的面积为S,点P的运动时间为t秒,求S与t之间的函数关系式;
(3)如图2,连接AC,在第二象限内存在点M,使得以M、O、A为顶点的三角形与△AOC相似.请直接写出所有符合条件的点M坐标.
【答案】
(1)解:∵抛物线y=ax2+bx+ ![]() 经过A(﹣3,0),B(1,0)两点,
经过A(﹣3,0),B(1,0)两点,
∴ ![]() ,
,
解得 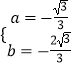 ,
,
∴抛物线解析式为y=﹣ ![]() x2﹣
x2﹣ ![]() x+
x+ ![]() ;
;
则D点坐标为(﹣2, ![]() )
)
(2)解:∵点D与A横坐标相差1,纵坐标之差为 ![]() ,则tan∠DAP=
,则tan∠DAP= ![]() ,
,
∴∠DAP=60°,
又∵△APQ为等边三角形,
∴点Q始终在直线AD上运动,当点Q与D重合时,由等边三角形的性质可知:AP=AD= ![]() .
.
①当0≤t≤2时,P在线段AO上,此时△APQ的面积即是△APQ与四边形AOCD的重叠面积.
AP=t,
∵∠QAP=60°,
∴点Q的纵坐标为tsin60°= ![]() t,
t,
∴S= ![]() ×
× ![]() t×t=
t×t= ![]() t2.
t2.
②当2<t≤3时,如图:
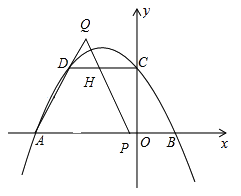
此时点Q在AD的延长线上,点P在OA上,
设QP与DC交于点H,
∵DC∥AP,
∴∠QDH=∠QAP=∠QHD=∠QPA=60°,
∴△QDH是等边三角形,
∴S=S△QAP﹣S△QDH,
∵QA=t,
∴S△QAP= ![]() t2.
t2.
∵QD=t﹣2,
∴S△QDH= ![]() (t﹣2)2,
(t﹣2)2,
∴S= ![]() t2﹣
t2﹣ ![]() (t﹣2)2=
(t﹣2)2= ![]() ﹣
﹣ ![]() .
.
③当3<t≤4时,如图:
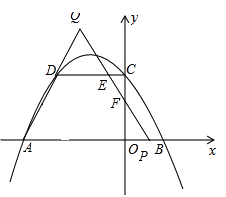
此时点Q在AD的延长线上,点P在线段OB上,
设QP与DC交于点E,与OC交于点F,过点Q作AP的垂涎,垂足为G,
∵OP=t﹣3,∠FPO=60°,
∴OF=OPtan60°= ![]() t﹣3),
t﹣3),
∴S△FOP= ![]() ×
× ![]() (t﹣3)(t﹣3)=
(t﹣3)(t﹣3)= ![]() (t﹣3)2,
(t﹣3)2,
∵S=S△QAP﹣S△QDE﹣S△FOP,S△QAP﹣S△QDE= ![]() t﹣
t﹣ ![]() .
.
∴S= ![]() t﹣
t﹣ ![]() ﹣
﹣ ![]() (t﹣3)2=
(t﹣3)2= ![]() t2+4
t2+4 ![]() t﹣
t﹣ ![]() .
.
综上所述,S与t之间的函数关系式为 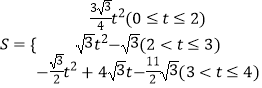
(3)解:∵OC= ![]() ,OA=3,OA⊥OC,则△OAC是含30°的直角三角形.
,OA=3,OA⊥OC,则△OAC是含30°的直角三角形.
①当△AMO以∠AMO为直角的直角三角形时;如图,过点M2作AO的垂线,垂足为N,
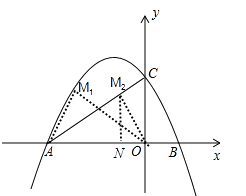
∵∠M2AO=30°,AO=3,
∴M2O= ![]() ,
,
又∵∠OM2N=M2AO=30°,
∴ON= ![]() OM2=
OM2= ![]() ,M2N=
,M2N= ![]() ON
ON ![]() ,
,
∴M2的坐标为(﹣ ![]() ,
, ![]() ).
).
同理可得M1的坐标为(﹣ ![]() ,
, ![]() ).
).
②当△AMO以∠OAM为直角的直角三角形时;如图:
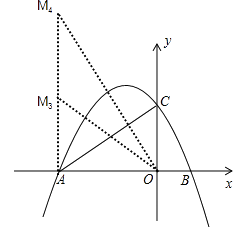
∵以M、O、A为顶点的三角形与△OAC相似,
∴ ![]() ,或
,或 ![]() =
= ![]() ,
,
∵OA=3,
∴AM= ![]() 或AM=
或AM= ![]() ,
,
∵AM⊥OA,且点M在第二象限,
∴点M的坐标为(﹣3, ![]() )或(﹣3,3
)或(﹣3,3 ![]() ).
).
综上所述,符合条件的点M的所有可能的坐标为(﹣3, ![]() ),(﹣3,3
),(﹣3,3 ![]() ),(
),( ![]() ,
, ![]() ,(﹣
,(﹣ ![]() ,
, ![]() ).
).
【解析】(1)把A、B两点的坐标代入抛物线解析式,求出抛物线的解析式,由抛物线与y轴交于点C,点D与点C关于抛物线的对称轴对称,由顶点式得到D点坐标;(2)由点D与A横坐标相差1,纵坐标之差为 3 ,得到tan∠DAP= 3 ,∠DAP=60°,又△APQ为等边三角形,得到点Q始终在直线AD上运动,当点Q与D重合时,由等边三角形的性质和勾股定理求出:AP=AD的值;①当0≤t≤2时,P在线段AO上,此时△APQ的面积即是△APQ与四边形AOCD的重叠面积;②当2<t≤3时,此时点Q在AD的延长线上,点P在线段OB上,根据已知条件和三角形的面积公式,得到S与t之间的三种函数关系式;(3)根据已知可得△OAC是含30°的直角三角形,①当△AMO以∠AMO为直角的直角三角形时,根据在直角三角形中,30度角所对的边是斜边的一半,求出M2的坐标,同理可得M1的坐标;②当△AMO以∠OAM为直角的直角三角形时,以M、O、A为顶点的三角形与△OAC相似,得到比例,求出AM的值,得到点M的坐标;此题是综合题,难度较大,计算和解方程时需认真仔细.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
【题目】某超市为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、"10元”、“20元”、“30元”的字样.规定:顾客在本超市一次性消费满200元,就可以在箱子里先后摸出两个小球(每一次摸出后不放回).某顾客刚好消费200元,则该顾客所获得购物券的金额不低于30元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场用36万元购进A、B两种商品,销售完后共获利6万元,其进价和售价如下表:
A | B | |
进价(元/件) | 1200 | 1000 |
售价(元/件) | 1380 | 1200 |
(注:获利=售价-进价)
(1) 该商场购进A、B两种商品各多少件?
(2) 商场第二次以原进价购进A、B两种商品.购进B种商品的件数不变,而购进A种商品的件数是第一次的2倍,A种商品按原价出售,而B种商品打折销售.若两种商品销售完毕,要使第二次经营活动获利不少于81600元,B种商品最低售价为每件多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的周长为30cm,点D、E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=11cm,则DE的长为____cm.
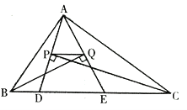
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,△ABC在平面直角坐标系中的位置如图所示
(1)、写出A、B、C三点的坐标
(2)、求△ABC的面积
(3)、△ABC中任意一点P(x0,y0)经平移后对应点为P1(x0+4,y0-3),将△ABC作同样的平移得到△A1B1C1,写出A1 、B1、C1的坐标
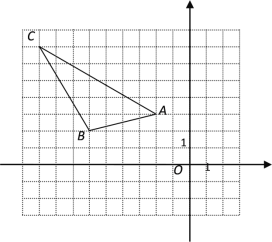
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】星期日早晨,小青从家出发匀速去森林公园溜冰,小青出发一段时间后,他妈妈发现小青忘带了溜冰鞋,于是立即骑自行车沿小青行进的路线匀速去追赶,妈妈追上小青后,立即沿原路线匀速返回家,但由于路上行人渐多,妈妈返回时骑车的速度只是原来速度的三分之二,小青继续以原速度步行前往森林公园,妈妈与小青之间的路程![]() 米
米![]() 与小青从家出发后步行的时间
与小青从家出发后步行的时间![]() 分
分![]() 之间的关系如图所示,当妈妈刚回到家时,小青到森林公园的路程还有______米
之间的关系如图所示,当妈妈刚回到家时,小青到森林公园的路程还有______米![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l:![]() 为常数,且
为常数,且![]() 经过第四象限.
经过第四象限.

(1)若直线l与x轴交于点![]() ,求m的值;
,求m的值;
(2)求m的取值范围:
(3)判断点![]() 是否在直线l上,若不在,判断在直线l的上方还是下方?请说明理由.
是否在直线l上,若不在,判断在直线l的上方还是下方?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】你能化简(x-1)(x99+x98+x97+…+x+1)吗?遇到这样的问题,我们可以先思考一下,从简单的情形入手,然后归纳出一些方法.
(1)分别化简下列各式:
①(x-1)(x+1)=___________;
②(x-1)(x2+x+1)=___________;
③(x-1)(x3+x2+1)=___________;
……
由此我们可以得到:(x-1)(x99+x98+x97+…+x+1)=________________.
(2)请你利用上面的结论计算:
299+298+297+…+2+1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的函数图象反映的过程是:李大爷每天早上都到公园锻炼,他从家去公园锻炼一会儿,又去了菜市场后马上回家,其中![]() 表示时间,
表示时间,![]() 表示李大爷离他家的距离。
表示李大爷离他家的距离。
(1)李大爷家到公园的距离是多少千米,他在公园银炼了多少小时;
(2)李大爷从菜市场回家的平均速度;
(3)李大爷从家到菜市场的平均速度。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com