
【题目】△ABC在平面直角坐标系中的位置如图所示.
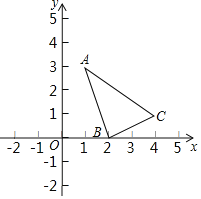
(1)分别写出下列三点坐标:A ,B ,C ;
(2)将△ABC平移至△OB′C′位置,使点A与原点O重合,画出平移后的△OB′C′,写出B′、C′的坐标;
(3)求△OB′C′的面积.
【答案】(1)(1,3)、(2,0)、(4,1);(2)如图所示,△OB′C′即为所求,见解析;B′(1,﹣3)、C′(3,﹣2).(3)△OB′C′的面积为![]() .
.
【解析】
(1)根据点在平面直角坐标系的位置,可分别写出点所对应的坐标即可;
(2)根据平移前后点A与对应点O坐标的位置,可以得出图形△ABC向左平移1个单位、向下平移3个单位,由此可得出平移后点B′、C′的坐标;
(3)利用割补法,把△OB′C′补成一个正方形,减去三个直角三角形的面积计算即可.
(1)由图形知A(1,3),B(2,0),C(4,1);
故答案为:(1,3)、(2,0)、(4,1);
(2)由A(1,3)及其对应点O(0,0)知,需将△ABC向左平移1个单位、向下平移3个单位,
如图所示,△OB′C′即为所求,其中B′(1,﹣3)、C′(3,﹣2),
故答案为:B′(1,﹣3)、C′(3,﹣2);

(3)△OB′C′的面积为3×3﹣![]() ×1×3﹣
×1×3﹣![]() ×3×2﹣
×3×2﹣![]() ×1×2=
×1×2=![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
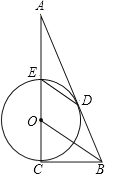
【题目】如图,CE是⊙O的直径,BC切⊙O于点C,连接OB,作ED∥OB交⊙O于点D,BD的延长线与CE的延长线交于点A.
(1)求证:AB是⊙O的切线;
(2)若⊙O的半径为1,tan∠DEO=![]() ,tan∠A=
,tan∠A=![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】元旦是公历新一年的第一天.“元旦”一词最早出现于《晋书》:“颛帝以孟夏正月为元,其实正朔元旦之春.”中国古代曾以腊月、十月等的月首为元旦,1949年中华人民共和国以公历1月1日为元旦,因此元旦在中国也被称为“阳历年”.为庆祝元旦,太原某商场举行促销活动,促销的方法是“消费超过200元时,所购买的商品按原价打8折后,再减少20元”.若某商品的原价为![]() 元,则购买该商品实际付款的金额是( )
元,则购买该商品实际付款的金额是( )
A.![]() 元B.
元B.![]() 元C.
元C.![]() 元D.
元D.![]() 元
元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于点D,DE⊥AB于点E,
(1)求证:AC=AE.
(2)若△BDE的周长是5cm,AB的长度为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市居民生活用水的费用由“城市供水费” 和“污水处理费”两部分组成.为了鼓励市民节约用水, 其中城市供水费按阶梯式计费:一个月用水 10 吨以内(包括 10 吨)的用户,每吨收 1.5 元;一个月用水超过 10 吨的用户,10 吨水仍按每吨 1.5 元收费,超过 10 吨的部分,按每吨 2 元收费.另外污水处理费按每吨 0.65 元收取.
(1)某居民 5 月份用水 8 吨,应交水费多少元?
(2)某居民 6 月份用水 12 吨,应交水费多少元?
(3)若某户某月用水 x 吨,请你用含有 x 的代数式表示该月应交的水费
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(1,a),将线段OA平移至线段BC,B(b,0),a是m+6n的算术平方根,![]() =3,n=
=3,n=![]() ,且m<n,正数b满足(b+1)2=16.
,且m<n,正数b满足(b+1)2=16.
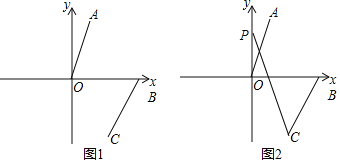
(1)直接写出A、B两点坐标为:A ,B ;
(2)如图1,连接AB、OC,求四边形AOCB的面积;
(3)如图2,若∠AOB=a,点P为y轴正半轴上一动点,试探究∠CPO与∠BCP之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用一个平面去截正方体(如图),下列关于截面(截出的面)形状的结论:
①可能是锐角三角形;②可能是钝角三角形;
③可能是长方形;④可能是梯形.
其中正确结论的是______(填序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读思考:
数学课上老师出了一道分式化简求值题目.
题目:![]() ÷(x+1)·
÷(x+1)·![]() -
-![]() ,其中x=-
,其中x=-![]() .
.
“勤奋”小组的杨明同学展示了他的解法:
解:原式=![]() -
-![]() ..................第一步
..................第一步
=![]() -
-![]() ................ ..第二步
................ ..第二步
=![]() ..........................第三步
..........................第三步
=![]() ..................................第四步
..................................第四步
当x=-![]() 时,原式=
时,原式= .......................第五步
.......................第五步
请你认真阅读上述解题过程,并回答问题:
你认为该同学的解法正确吗?如有错误,请指出错误在第几步,并写出完整、正确的解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
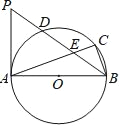
【题目】如图,AB是⊙O的直径,BC为弦,D为弧AC的中点,AC、BD相交于点E.AP交BD的延长线于点P.∠PAC=2∠CBD.
(1)求证:AP是⊙O的切线;
(2)若PD=3,AE=5,求△APE的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com