
【题目】已知点A(1,a),将线段OA平移至线段BC,B(b,0),a是m+6n的算术平方根,![]() =3,n=
=3,n=![]() ,且m<n,正数b满足(b+1)2=16.
,且m<n,正数b满足(b+1)2=16.
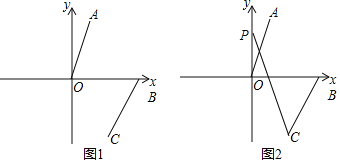
(1)直接写出A、B两点坐标为:A ,B ;
(2)如图1,连接AB、OC,求四边形AOCB的面积;
(3)如图2,若∠AOB=a,点P为y轴正半轴上一动点,试探究∠CPO与∠BCP之间的数量关系.
【答案】(1)A(1,3); B(3,0);(2)S四边形AOCB=9;(3)∠BCP﹣∠CPO=90°﹣a.
【解析】
(1)根据算术平方根、二次根式和偶次幂解答即可;
(2)根据平移的性质和三角形的面积解答即可;
(3)过点P作PD∥OA,可证得PD∥OA∥BC,由平行线的性质进行解答即可.
(1)∵a是m+6n的算术平方根,![]() =3,n=
=3,n=![]() ,且m<n,正数b满足(b+1)2=16.
,且m<n,正数b满足(b+1)2=16.
∴m=﹣3,n=2,a=3,b=3,
∴A(1,3),B(3,0);
故答案为:A(1,3); B(3,0);
(2)如图1所示:
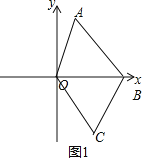
由题意知:C(2,﹣3),
∵B(3,0),
∴OB=3,
∴S四边形AOCB=S△AOB+S△BOC=![]() ,
,
故答案为:9;
(3)过点P作PD∥OA,如图2所示:
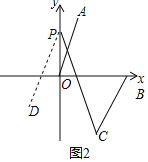
∵OA∥BC,
∴PD∥OA∥BC
∴∠BCP=∠DPC,∠DPO=∠AOP.
∵∠AOB=a,
∴∠AOP=90°﹣∠AOB=90°﹣a.
∴∠DPO=90°﹣a.
∵∠DPC=∠DPO+∠CPO,
∴∠BCP=∠CPO+90°﹣a,
即∠BCP﹣∠CPO=90°﹣a,
故答案为:∠BCP﹣∠CPO=90°﹣a.


科目:初中数学 来源: 题型:
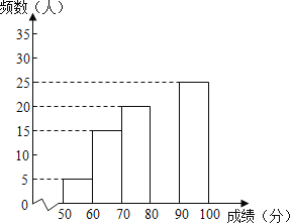
【题目】某学校七年级举行“每天锻炼一小时,健康生活一辈子”为主题的一分钟跳绳大赛,校团委组织了全级1000名学生参加为了解本次大赛的成绩,校团委随机抽取了其中100名学生的成绩作为样本进行统计,制成如下不完整的统计图表根据所给信息,解答下列问题;
(1)m=______,n=______.
(2)补全频数分布直方图;
(3)若成绩在80分以上(包括80分)为“优”,请你估计该校七年级参加本次比赛的1000名学生中成绩是“优”的有多少人.
成绩x(分) | 频数(人) | 频率 |
50≤x<60 | 5 | 5% |
60≤x<70 | 15 | 15% |
70≤x<80 | 20 | 20% |
80≤x<90 | m | 35% |
90≤x≤100 | 25 | n |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=50 cm,BC=40 cm,∠C=90°,点P从点A开始沿AC边向点C以2 cm/s的速度匀速运动,同时另一点Q由点C开始以3 cm/s的速度沿着CB向点B匀速运动,当其中一点到达终点时,另一点也随之停止运动,则当△PCQ的面积等于300 cm2时,运动时间为( )

A. 5 s B. 20 s C. 5 s或20 s D. 不确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于正整数 n ,我们定义一种“运算”:①当 n 为奇数时,结果为 n 1;②当 n 为偶数时,结果为![]() ,并且运算重复进行.例如,取 n 9 ,则
,并且运算重复进行.例如,取 n 9 ,则
![]()
若 n 12 ,则第 2019 次运算的结果是( )
A.2018B.2017C.2D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中的位置如图所示.
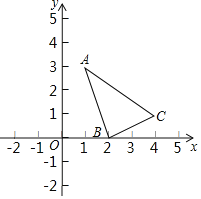
(1)分别写出下列三点坐标:A ,B ,C ;
(2)将△ABC平移至△OB′C′位置,使点A与原点O重合,画出平移后的△OB′C′,写出B′、C′的坐标;
(3)求△OB′C′的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
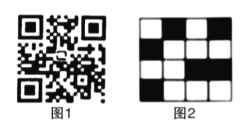
【题目】利用如图1的二维码可以进行身份识别.某校建立了一个身份识别系统,图2是某个学生的识别图案,黑色小正方形表示1,白色小正方形表示0,将第一行数字从左到右依次记为![]() ,那么可以转换为该生所在班级序号,其序号为
,那么可以转换为该生所在班级序号,其序号为![]() (注:
(注:![]() ),如图2第一行数字从左到右依次为0,1,0,1,序号为
),如图2第一行数字从左到右依次为0,1,0,1,序号为![]() ,表示该生为5班学生,那么表示7班学生的识别图案是( )
,表示该生为5班学生,那么表示7班学生的识别图案是( )
A. B.
B.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边△ABC的顶点A、C处各有一只蜗牛,它们同时出发,分别以每分钟1米的速度由A向B和由C向A爬行,其中一只蜗牛爬到终点时,另一只也停止运动,经过t分钟后,它们分别爬行到D、E处,请问:
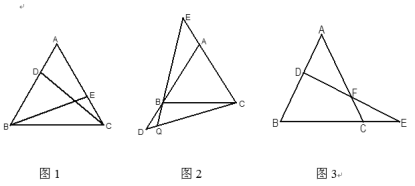
(1)如图1,在爬行过程中,CD和BE始终相等吗?
(2)如果将原题中的“由A向B和由C向A爬行”,改为“沿着AB和CA的延长线爬行”,EB与CD交于点Q,其他条件不变,蜗牛爬行过程中∠CQE的大小保持不变,请利用图2说明:∠CQE=60°;
(3)如果将原题中“由C向A爬行”改为“沿着BC的延长线爬行,连接DE交AC于F”,其他条件不变,如图3,则爬行过程中,DF始终等于EF是否正确?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春季是传染病多发的季节,积极预防传染病是学校高度重视的一项工作,为此,某校对学生宿舍采取喷洒药物进行消毒.在对某宿舍进行消毒的过程中,先经过![]() 的集中药物喷洒,再封闭宿舍
的集中药物喷洒,再封闭宿舍![]() ,然后打开门窗进行通风,室内每立方米空气中含药量
,然后打开门窗进行通风,室内每立方米空气中含药量![]() 与药物在空气中的持续时间
与药物在空气中的持续时间![]() 之间的函数关系,在打开门窗通风前分别满足两个一次函数,在通风后又成反比例,如图所示.下面四个选项中错误的是( )
之间的函数关系,在打开门窗通风前分别满足两个一次函数,在通风后又成反比例,如图所示.下面四个选项中错误的是( )

A. 经过![]() 集中喷洒药物,室内空气中的含药量最高达到
集中喷洒药物,室内空气中的含药量最高达到![]()
B. 室内空气中的含药量不低于![]() 的持续时间达到了
的持续时间达到了![]()
C. 当室内空气中的含药量不低于![]() 且持续时间不低于35分钟,才能有效杀灭某种传染病毒.此次消毒完全有效
且持续时间不低于35分钟,才能有效杀灭某种传染病毒.此次消毒完全有效
D. 当室内空气中的含药量低于![]() 时,对人体才是安全的,所以从室内空气中的含药量达到
时,对人体才是安全的,所以从室内空气中的含药量达到![]() 开始,需经过
开始,需经过![]() 后,学生才能进入室内
后,学生才能进入室内
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com