练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】求证：全等三角形对应的角平分线相等。

    【答案】证明见详解

    【解析】

    作出图形，结合图形写出已知、求证，根据全等三角形对应边相等、对应角相等，AB=A′B′，∠B=∠B′，∠BAC=∠B′A′C′，又AD、A′D′是∠BAC和∠B′A′C′的平分线，所以∠BAD=∠B′A′D′，根据角边角判定定理可得△ABD和△A′B′D′全等，所以角平分线AD、A′D′相等．

    已知：如图，△ABC≌△A′B′C′，AD、A′D′是∠BAC和∠B′A′C′的平分线，

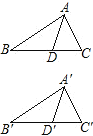
    求证：AD=A′D′，

    证明：∵△ABC≌△A′B′C′，

    ∴∠B=∠B′，AB=A′B′，

    ∠BAC=∠B′A′C′，

    ∵AD平分∠BAC，A′D′平分∠B′A′C′，

    ∴∠BAD=∠B′A′D′，

    ∴△ABD≌△A′B′D′，

    ∴AD=A′D′．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，直线l为正比例函数y=x的图象，点A1的坐标为（1，0），过点A1作x轴的垂线交直线l于点D1，以A1D1为边作正方形A1B1C1D1；过点C1作直线l的垂线，垂足为A2，交x轴于点B2，以A2B2为边作正方形A2B2C2D2；过点C2作x轴的垂线，垂足为A3，交直线l于点D3，以A3D3为边作正方形A3B3C3D3，…，按此规律操作下所得到的正方形AnBnCnDn的面积是_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠C＝90°，AC＝BC，AD平分∠BAC交BC于点D，DE⊥AB于点E，

    (1)求证：AC=AE.

    (2)若△BDE的周长是5cm，AB的长度为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知点A（1，a），将线段OA平移至线段BC，B（b，0），a是m+6n的算术平方根，＝3，n＝，且m＜n，正数b满足（b+1）2＝16．

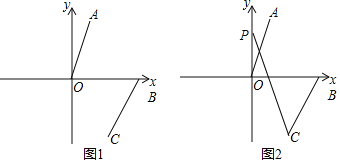
    （1）直接写出A、B两点坐标为：A　 　，B　 　；

    （2）如图1，连接AB、OC，求四边形AOCB的面积；

    （3）如图2，若∠AOB＝a，点P为y轴正半轴上一动点，试探究∠CPO与∠BCP之间的数量关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】用一个平面去截正方体（如图），下列关于截面（截出的面）形状的结论：

    ①可能是锐角三角形；②可能是钝角三角形；

    ③可能是长方形；④可能是梯形．

    其中正确结论的是______（填序号）.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校积极开展“阳光体育进校园”活动，决定开设 A：乒乓球，B：篮球，C：跑步，D：跳绳四种运动项目，规定每个学生必须参加一项活动。学校为了了解学生最喜欢哪一种运动项目，设计了以下四种调查方案.

    方案一：调查该校七年级女生喜欢的运动项目

    方案二：调查该校每个班级学号为 5 的倍数的学生喜欢的运动项目

    方案三：调查该校书法小组的学生喜欢的运动项目

    方案四：调查该校田径队的学生喜欢的运动项目

    （1）上面的调查方案最合适的是 ；

    学校体育组采用了（1）中的方案，将调查的结果绘制成如下两幅不完整的统计图表.

    最喜欢的运动项目人数调查统计表 最喜欢的运动项目人数分布统计图

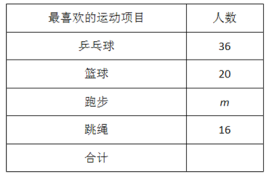
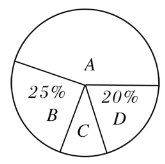
    请你结合图表中的信息解答下列问题：

    （2）这次抽样调查的总人数是 ，m＝ ；

    （3）在扇形统计图中，A 项目对应的圆心角的度数为 ；

    （4）已知该校有 1200 名学生，请根据调查结果估计全校学生最喜欢乒乓球的人数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读思考：

    数学课上老师出了一道分式化简求值题目．

    题目：÷(x＋1)·－，其中x＝－.

    “勤奋”小组的杨明同学展示了他的解法：

    解：原式＝－ ..................第一步

    ＝－ ................ ..第二步

    ＝ ..........................第三步

    ＝ ..................................第四步

    当x＝－时，原式＝ .......................第五步

    请你认真阅读上述解题过程，并回答问题：

    你认为该同学的解法正确吗？如有错误，请指出错误在第几步，并写出完整、正确的解答过程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图是一个无理数筛选器的工作流程图．

    （1）当时，的值为_____________；

    （2）是否存在输入有意义的的值后，却输不出的值？如果存在，写出所有满足要求的的值；如果不存在，请说明理由；

    （3）当输出的的值是时，判断输入的的值是否唯一，如果不唯一，请写出其中的个．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，D为等边△ABC内的一点，AD＝BD，BP＝AB，∠DBP＝∠DAC，若∠DBC＝15°，则∠ADP的度数是__________

    查看答案和解析>>

    同步练习册答案