
分析 (1)设乙型号显示器连续两次降价的百分率为x,根据乙型号的显示器价格经过两次降价,由400元/台降到225元/台,列出方程,再求解即可;
(2)设甲型显示器的台数为x台,根据购进甲种显示器的台数至少为23台和甲型显示器的台数不超过乙型显示器的台数,列出不等式组,求解即可.
解答 解:(1)设乙型号显示器连续两次降价的百分率为x,根据题意得:
400(1-x)2=225,
解得:x1=0.25=25%,x2=1.75(不合题意,舍去),
答:乙型号显示器连续两次降价的百分率为25%;
(2)设甲型显示器的台数为x台,根据题意得;
$\left\{\begin{array}{l}{x≥23}\\{x≤50-x}\end{array}\right.$,
解得:23≤x≤25,
∵x为正整数,
∴x=23,24,25,
∴有3种购买方案,
方案①:甲型显示器23台,乙型显示器27台;
方案②:甲型显示器24台,乙型显示器26台;
方案③:甲型显示器25台,乙型显示器25台.
点评 此题考查了一元二次方程和一元一次不等式组的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程和不等式组,再求解;注意把不合题意的解舍去.


科目:初中数学 来源:2016-2017学年四川达县万家中学下学期九年级第一次月考数学试卷(解析版) 题型:填空题
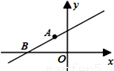
如图,直线y=kx+b经过A(﹣1,1)和B(﹣3,0)两点,则关于x的不等式组0<kx+b<﹣x的解集为_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
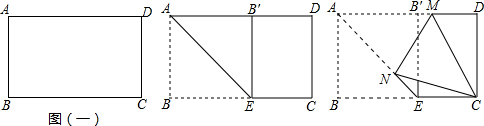
| A. | 6-2$\sqrt{3}$ | B. | 3$\sqrt{2}$-6 | C. | 6$\sqrt{3}$-6 | D. | $\sqrt{3}$+$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
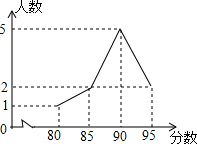 在“大家跳起来”的学校跳操比赛中,九年级参赛的10名学生成绩统计如图所示,对于这10名学生的参赛成绩,下列说法中错误的是( )
在“大家跳起来”的学校跳操比赛中,九年级参赛的10名学生成绩统计如图所示,对于这10名学生的参赛成绩,下列说法中错误的是( )| A. | 众数是90分 | B. | 中位数是90分 | C. | 平均数是90分 | D. | 极差是15分 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com