
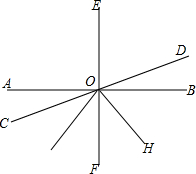
 如图,AB、CD、EF相交于点O,EF⊥AB,OG平分∠COF,OH平分∠DOG,若∠AOC:∠DOH=8:29,求∠COH的大小.
如图,AB、CD、EF相交于点O,EF⊥AB,OG平分∠COF,OH平分∠DOG,若∠AOC:∠DOH=8:29,求∠COH的大小. 分析 由∠DOB=90°-2∠COG,∠DOB:[$\frac{1}{2}$(180°-∠COG]=8:29组成方程即可得出∠COG的度数,代入求出∠DOH,即可求出∠COH.
解答 解:∵∠AOC=∠DOB,
∴∠DOB=90°-2COF=90°-2∠COG,
∵OH为∠DOG的平分线,
∴$\frac{1}{2}$(180°-∠COG)=∠DOH,
∵∠AOC:∠DOH=8:29,
∴∠DOB:[$\frac{1}{2}$(180°-∠COG]=8:29,
解得∠DOB=20°,∠COG=35°,
∴$\frac{1}{2}$(180°-∠COG)=∠DOH=72.5°,
∴∠COH=180°-72.5°=107.5°.
点评 本题主要考查了垂线及角平分线的定义,解题的关键是根据垂线及角平分线的定义列出式子求解.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
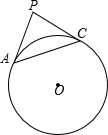 如图,已知⊙O的半径是4,AC是⊙0的弦,AP是⊙0的切线,AC=4$\sqrt{2}$,AP=4,连接PC,判断直线PC和⊙0的位置关系,并说明理由.
如图,已知⊙O的半径是4,AC是⊙0的弦,AP是⊙0的切线,AC=4$\sqrt{2}$,AP=4,连接PC,判断直线PC和⊙0的位置关系,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
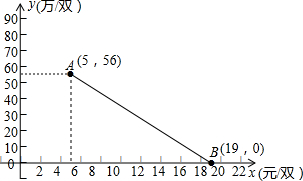 某袜业公司向上海世博会申请了在自己生产的袜子上印上海世博会会徽的专利权,但组委会只允许这种袜子在5月1日至5月31日这一个月内在全国各地生产销售.生产这种袜子的成本为每双5元,该袜业公司经过一段时间调查与分所后,发现这种袜子在5月份销售期间,每双袜子的销售单价x(元)和日均销售量y(万双)满足如图所示关系;日均各种费用等固定成本为20万元.
某袜业公司向上海世博会申请了在自己生产的袜子上印上海世博会会徽的专利权,但组委会只允许这种袜子在5月1日至5月31日这一个月内在全国各地生产销售.生产这种袜子的成本为每双5元,该袜业公司经过一段时间调查与分所后,发现这种袜子在5月份销售期间,每双袜子的销售单价x(元)和日均销售量y(万双)满足如图所示关系;日均各种费用等固定成本为20万元.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com