练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    14．在△ABC中，∠A、∠B、∠C所对的边分别为a，b，c，若a2+c2=b2，则∠B=90°．

    分析 勾股定理的逆定理：如果三角形的三边长a，b，c满足a2+c2=b2，那么这个三角形就是直角三角形．

    解答 解：∵在△ABC中，∠A，∠B，∠C的对边分别是a，b，c，三边关系为a2+c2=b2，
    ∴∠B是直角．
    故答案为：∠B．

    点评 本题考查了勾股定理的逆定理，运用勾股定理的逆定理解决问题的实质就是判断一个角是不是直角．然后进一步结合其他已知条件来解决问题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    4．观察下列等式：
    第一个等式：a1=$\frac{3}{1×2×{2}^{2}}$=$\frac{1}{1×2}$-$\frac{1}{2×{2}^{2}}$；
    第二个等式：a2=$\frac{4}{2×3×{2}^{3}}$=$\frac{1}{2×{2}^{2}}$-$\frac{1}{3×{2}^{3}}$；
    第三个等式：a3=$\frac{5}{3×4×{2}^{4}}$=$\frac{1}{3×{2}^{3}}$-$\frac{1}{4×{2}^{4}}$；
    第四个等式：a4=$\frac{6}{4×5×{2}^{5}}$=$\frac{1}{4×{2}^{4}}$-$\frac{1}{5×{2}^{5}}$．
    按上述规律，则式子a1+a2+a3+…+a22的结果为（　　）
    A．$\frac{1}{2}-\frac{1}{{21×{2^{21}}}}$B．$\frac{1}{2}-\frac{1}{{22×{2^{22}}}}$C．$\frac{1}{2}-\frac{1}{{23×{2^{23}}}}$D．$\frac{1}{2}-\frac{1}{{24×{2^{24}}}}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．数轴是一个非常重要的数学工具，它使数和数轴上的点建立其对应关系，展示了数与点之间的内在联系，它是“数形结合”的基础．
    思考：
    （1）数轴上表示1和-3的两点之间的距离是4．
    （2）若|x-2|=1，利用绝对值的几何意义可得x=3或1．
    （3）若x表示一个有理数，则|x-1|+|x+3|的最小值为4．
    （4）画数轴并在数轴上标出点A：-7，B：-3，C：2，D：6，．若点P在数轴上，则点P到这四点的距离总和的最小值是18，且点P在线段BC上．
    应用：
    某一直线沿街有2014户居民（相邻两户居民间隔相同）：a1，a2，a3，a4，a5，…a2014，某餐饮公司想为这2014户居民提供早餐，决定在路旁建立一个快餐店P，点P选在何处，才能使这2014户居民到点P的距离总和最小？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

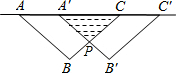    2．如图，把等腰Rt△ABC沿AC方向平移到等腰Rt△A′B′C′的位置时，它们重叠的部分的面积是Rt△ABC面积的$\frac{1}{4}$．若AB=$\sqrt{2}$cm，则它移动的距离AA′=1cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．当x=3时，（x2-x）-（x2+2x）+1的值等于（　　）
    A．8B．-8C．-6D．6

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．已知整式6x-1的值是2，y2-y的值是2，则（5x2y+5xy-7x）-（4x2y+5xy-7x）的值是$\frac{1}{2}$或-$\frac{1}{4}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．如图，AB、CD、EF相交于点O，EF⊥AB，OG平分∠COF，OH平分∠DOG，若∠AOC：∠DOH=8：29，求∠COH的大小．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．菱形有一个内角为120°，较短对角线为6，则菱形的周长为（　　）
    A．12B．24C．36D．12$\sqrt{3}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．小明在楼顶上看到对面山上有一座铁塔．他现有的测量材料：测倾器、皮尺．请你根据你所掌握的知识，选择恰当的条件求出塔高．（精确到1）
    ∠DEB=22°，∠CEB=9°，∠DAB=33°，∠CAB∠=14°，∠DFG=42°
    （参考数据：tan22°≈0.40，tan9°≈0.16，tan33°≈0.65，tan14°≈0.25，tan42°≈0.90）
    根据你的发现，在下面的题中填入所需要的条件（只做一题），并解答．
    （1）选两个长度，角度任选．
    已知：AE=120m，AB=200m，∠DEB=22°，∠CEB=9°
    求：CD．
    （2）选一个长度，角度任选．
    已知：AB=200m，∠CAB=14°，∠DAB=33°
    求：CD．
    我选（2）．解答如下：在Rt△DAB中DB=AB•tag33°=200×0.65=130m，
    在Rt△CAB中BC=AB•tag14°=200×0.25=50m，
    ∴CD=DB-BC=130-50=80m．．

    查看答案和解析>>

    同步练习册答案