
| A. | $\frac{1}{2}-\frac{1}{{21×{2^{21}}}}$ | B. | $\frac{1}{2}-\frac{1}{{22×{2^{22}}}}$ | C. | $\frac{1}{2}-\frac{1}{{23×{2^{23}}}}$ | D. | $\frac{1}{2}-\frac{1}{{24×{2^{24}}}}$ |
分析 根据已知的四个等式可以得出数字之间的规律,然后利用规律写出第a22个等式,将这些等式相加发现,除了第一项和最后一项外,其余都可以抵消,进而可以得出答案.
解答 解:观察已知等式:
第一个等式:a1=$\frac{3}{1×2×{2}^{2}}$=$\frac{1}{1×2}$-$\frac{1}{2×{2}^{2}}$;
第二个等式:a2=$\frac{4}{2×3×{2}^{3}}$=$\frac{1}{2×{2}^{2}}$-$\frac{1}{3×{2}^{3}}$;
第三个等式:a3=$\frac{5}{3×4×{2}^{4}}$=$\frac{1}{3×{2}^{3}}$-$\frac{1}{4×{2}^{4}}$;
第四个等式:a4=$\frac{6}{4×5×{2}^{5}}$=$\frac{1}{4×{2}^{4}}$-$\frac{1}{5×{2}^{5}}$.
得出a22=$\frac{24}{22×23×{2}^{23}}$=$\frac{1}{22×{2}^{22}}$-$\frac{1}{23×{2}^{23}}$
∴a1+a2+a3+…+a22
=$\frac{1}{1×2}$-$\frac{1}{2×{2}^{2}}$+$\frac{1}{2×{2}^{2}}$-$\frac{1}{3×{2}^{3}}$+$\frac{1}{3×{2}^{3}}$-$\frac{1}{4×{2}^{4}}$+…+$\frac{1}{22×{2}^{22}}$-$\frac{1}{23×{2}^{23}}$
=$\frac{1}{1×2}$-$\frac{1}{23×{2}^{23}}$
=$\frac{1}{2}$-$\frac{1}{23×{2}^{23}}$.
故选:C.
点评 题目考查数字的变化规律,根据这些变化规律,写出相应关系式,可以得出相应结论.题目相对简单,但是对于考查学生的观察能力和解决问题能力有很大帮助.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
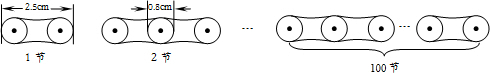
| A. | 250cm | B. | 174.5cm | C. | 170.8cm | D. | 172cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com