
 求如图所示的图形中小圆圈的总数.
求如图所示的图形中小圆圈的总数. 分析 观察图形,可以发现图形的组合非常规则,图形由中间蓝色正六边形和外部六个正三角形构成,首先计算一个正三角形圆圈个数,然后乘以6即可,然后在计算中间蓝色正六边形的圆圈个数,将两次求得圆圈个数相加即可.
解答 解:观察图形,可以看作图形由七部分组成,
即:中间蓝色正六边形和外部六个正三角形,
∵六个正三角形构成圆圈数一样,
∴六个正三角形圆圈总数:
(1+2+3+4)×6=10×6=60(个).
蓝色正六边形圆圈个数:
5+6+7+8+9+8+7+6+5
=10+12+14+16+9
=61(个)
∴图形中小圆圈的总数:
60+61=121(个)
答:图形中小圆圈的总数有121个
点评 题目考查图形的变化规律,通过观察图形就可以看出图形的组成,在计算圆圈个数的时候,可以适当利用等差数列的求和公式(如:sn=$\frac{({a}_{1}+{a}_{n})n}{2}$)简便运算.


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
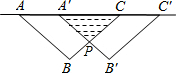 如图,把等腰Rt△ABC沿AC方向平移到等腰Rt△A′B′C′的位置时,它们重叠的部分的面积是Rt△ABC面积的$\frac{1}{4}$.若AB=$\sqrt{2}$cm,则它移动的距离AA′=1cm.
如图,把等腰Rt△ABC沿AC方向平移到等腰Rt△A′B′C′的位置时,它们重叠的部分的面积是Rt△ABC面积的$\frac{1}{4}$.若AB=$\sqrt{2}$cm,则它移动的距离AA′=1cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com