
【题目】如图所示的图象描述一辆汽车在直线行驶过程中,汽车离出发地的距离 s(千米)和行驶时间 t(小时)之间的函数关系.请根据图中提供的信息,完成下列问题:
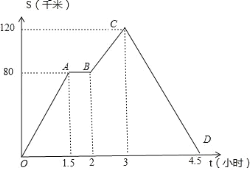
(1)汽车在 OA 段行驶的平均速度是_____km/h,在 BC 段行驶的平均速度是_____km/h,在 CD 段行驶的平均速度是_____km/h.
(2)AB 段表示的含义是_____.
(3)汽车全程所走路程是_____km.
【答案】![]() 40 80 汽车行驶到距离出发地 80 千米处停止,停留时间为 0.5 小时 240
40 80 汽车行驶到距离出发地 80 千米处停止,停留时间为 0.5 小时 240
【解析】
(1)根据函数图象中的数据结合速度=路程÷时间,列式计算即可;
(2)根据AB段S的值不变可以写出AB段表示的含义;
(3)根据函数图象中的数据计算即可.
解:(1)汽车在OA段行驶的平均速度是:80÷1.5=![]() km/h,
km/h,
在BC段行驶的平均速度是:(120-80)÷(3-2)=40km/h,
在CD段行驶的平均速度是:120÷(4.5-3)=80km/h,
故答案为:![]() ,40,80;
,40,80;
(2)AB段表示的含义是汽车行驶到距离出发地80千米处停止,停留时间为0.5小时,
故答案为:汽车行驶到距离出发地80千米处停止,停留时间为0.5小时;
(3)汽车全程所走路程是:120×2=240km,
故答案为:240.


科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:
①四边形AEGF是菱形②△AED≌△GED③∠DFG=112.5°④BC+FG=1.5其中正确的结论是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
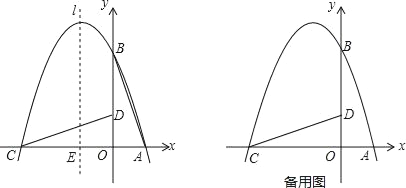
【题目】如图,在平面直角坐标系中有一直角三角形AOB,O为坐标原点,OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC,抛物线y=ax2+bx+c经过点A、B、C.
(1)求抛物线的解析式;
(2)若点P是第二象限内抛物线上的动点,其横坐标为t,设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求以C、E、F为顶点三角形与△COD相似时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
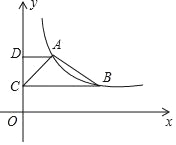
【题目】如图,在平面直角坐标系中,反比例函数y=![]() (x>0,k>0)的图象经过点A(1,a),B(m,n)(m>0),分别过A、B两点作y轴垂线,垂足分别为D,C,且CD=
(x>0,k>0)的图象经过点A(1,a),B(m,n)(m>0),分别过A、B两点作y轴垂线,垂足分别为D,C,且CD=![]() .
.
(1)求k关于n的关系式;
(2)当△ABC面积为2时,求反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
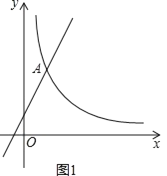
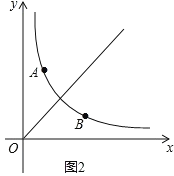
【题目】如图,已知点A是直线y=2x+1与反比例函数![]() (x>0)图象的交点,且点A的横坐标为1.
(x>0)图象的交点,且点A的横坐标为1.
(1)求k的值;
(2)如图1,双曲线![]() (x>0)上一点M,若S△AOM=4,求点M的坐标;
(x>0)上一点M,若S△AOM=4,求点M的坐标;
(3)如图2所示,若已知反比例函数![]() (x>0)图象上一点B(3,1),点P是直线y=x上一动点,点Q是反比例函数
(x>0)图象上一点B(3,1),点P是直线y=x上一动点,点Q是反比例函数![]() (x>0)图象上另一点,是否存在以P、A、 B、Q为顶点的平行四边形?若存在,请求出点Q的坐标;若不存在,请说明理由.
(x>0)图象上另一点,是否存在以P、A、 B、Q为顶点的平行四边形?若存在,请求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点 B、O分别落在点 B1、C1 处,点B1在x轴上,再将△AB1C1 绕点 B1 顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2 绕点C2 顺时针旋转到△A2B2C2 的位置,点 A2 在x轴上,依次进行下去….若点 A(![]() ,0),B(0,4),则点 B2016 的横坐标为_______.
,0),B(0,4),则点 B2016 的横坐标为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
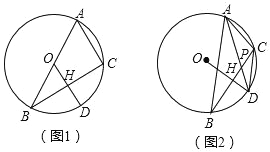
【题目】已知:△AC 内接于⊙O,D 是弧BC上一点,OD⊥BC,垂足为 H.
(1)如图 1,当圆心 O 在 AB 边上时,求证:AC=2OH;
(2)如图 2,当圆心 O 在△ABC 外部时,连接 AD、CD,AD 与 BC 交于点 P.求证:∠ACD=∠APB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】石狮泰禾某童装专卖店在销售中发现,一款童装每件进价为80元,销售价为120元时,每天可售出20件,为了迎接“十一”国庆节,商店决定采取适当的降价措施,以扩大销售量,增加利润,经市场调查发现,如果每件童装降价1元,那么平均可多售出2件.
(1)设每件童装降价x元时,每天可销售______ 件,每件盈利______ 元;(用x的代数式表示)
(2)每件童装降价多少元时,平均每天赢利1200元.
(3)要想平均每天赢利2000元,可能吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OM=2,MN=6,A为射线ON上的动点,以OA为一边作内角∠OAB=120°的菱形OABC,则BM+BN的最小值为 ( )

A. ![]() B. 6 C.
B. 6 C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com