
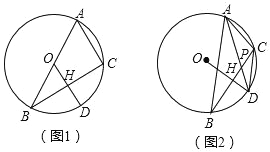
【题目】已知:△AC 内接于⊙O,D 是弧BC上一点,OD⊥BC,垂足为 H.
(1)如图 1,当圆心 O 在 AB 边上时,求证:AC=2OH;
(2)如图 2,当圆心 O 在△ABC 外部时,连接 AD、CD,AD 与 BC 交于点 P.求证:∠ACD=∠APB.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,某中学准备围建一个矩形苗圃,其中一边靠墙,另外三边用长为![]() 米的篱笆围成,若墙长为
米的篱笆围成,若墙长为![]() 米,设这个苗圃垂直于墙的一边长为
米,设这个苗圃垂直于墙的一边长为![]() 米.
米.

![]() 若苗圃园的面积为
若苗圃园的面积为![]() 平方米,求
平方米,求![]() 的值;
的值;
![]() 若平行于墙的一边长不小于
若平行于墙的一边长不小于![]() 米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值,如果没有,请说明理由.
米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值,如果没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,把△ABC绕AB边上的点D顺时针旋转,旋转角为α(0°<α<180°),得到Rt△A′DE,A′C′交AB于点E,若AD=BE,则AD的长为_____

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的图象描述一辆汽车在直线行驶过程中,汽车离出发地的距离 s(千米)和行驶时间 t(小时)之间的函数关系.请根据图中提供的信息,完成下列问题:
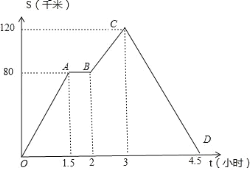
(1)汽车在 OA 段行驶的平均速度是_____km/h,在 BC 段行驶的平均速度是_____km/h,在 CD 段行驶的平均速度是_____km/h.
(2)AB 段表示的含义是_____.
(3)汽车全程所走路程是_____km.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着市民环保意识的增强,烟花爆竹销售量逐年下降,菏泽市2014年销售烟花爆竹20万箱,到2016年烟花爆竹销售量为9.8万箱.求菏泽市2014年到 2016年烟花爆竹销售量的平均下降率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知抛物线与直线的图象如图所示,则下列说法:
①当0<x<2时, y1>y2;②y1随x的增大而增大的取值范围是x<2;③使得y2大于4的x值不存在;④若y1=2,则x=2﹣![]() 或x=1.其中正确的有( )
或x=1.其中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形AOBC的边OB、OA分别在x、y轴上,点C坐标为(8,8),将正方形AOBC绕点A逆时针旋转角度α(0°<α<90°),得到正方形ADEF,ED交线段BC于点Q,ED的延长线交线段OB于点P,连接AP、AQ.
(1)求证:△ACQ≌△ADQ;
(2)求∠PAQ的度数,并判断线段OP、PQ、CQ之间的数量关系,并说明理由;
(3)连接BE、EC、CD、DB得到四边形BECD,在旋转过程中,四边形BECD能否是矩形?如果能,请求出点P的坐标,如果不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某消防队在一居民楼前进行演习,消防员利用云梯成功救出点B处的求救者后,又发现点B正上方点C处还有一名求救者.在消防车上点A处测得点B和点C的仰角分别是45°和65°,点A距地面2.5米,点B距地面10.5米.为救出点C处的求救者,云梯需要继续上升的高度BC约为多少米?(结果保留整数.参考数据:tan65°≈2.1,sin65°≈0.9,cos65°≈0.4,![]() ≈1.4)
≈1.4)

查看答案和解析>>
科目:初中数学 来源: 题型:
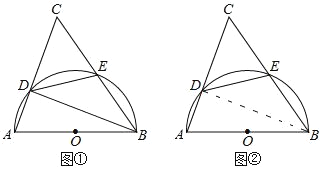
【题目】已知,△ABC中,∠A=68°,以AB为直径的⊙O与AC,BC的交点分别为D,E
(Ⅰ)如图①,求∠CED的大小;
(Ⅱ)如图②,当DE=BE时,求∠C的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com