
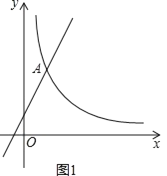
����Ŀ����ͼ����֪��A��ֱ��y=2x+1�뷴��������![]() (x��0)ͼ��Ľ��㣬�ҵ�A�ĺ�����Ϊ1��
(x��0)ͼ��Ľ��㣬�ҵ�A�ĺ�����Ϊ1��
(1)��k��ֵ��
(2)��ͼ1��˫����![]() (x��0)��һ��M����S��AOM=4�����M�����ꣻ
(x��0)��һ��M����S��AOM=4�����M�����ꣻ
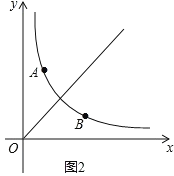
(3)��ͼ2��ʾ������֪����������![]() (x��0)ͼ����һ��B(3��1)����P��ֱ��y=x��һ���㣬��Q�Ƿ���������
(x��0)ͼ����һ��B(3��1)����P��ֱ��y=x��һ���㣬��Q�Ƿ���������![]() (x��0)ͼ������һ�㣬�Ƿ������P��A�� B��QΪ�����ƽ���ı���?�����ڣ��������Q�����ꣻ�������ڣ���˵�����ɣ�
(x��0)ͼ������һ�㣬�Ƿ������P��A�� B��QΪ�����ƽ���ı���?�����ڣ��������Q�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��k��3��2��M��3��1����M��![]() ��9����3��Q1��
��9����3��Q1��![]() ��2��
��2��![]() 2����Q2��
2����Q2��![]() 2��
2��![]() ��2����Q3��
��2����Q3��![]() ��
��![]() ����
����
��������
��1����A��ֱ��y��2x��1�ĵ㣬��A�ĺ�����Ϊ1������y��2��1��1��3����õ�A���ɵõ������
��2����ͼ1�����M��m��![]() ������A��AE��x����E����M��MF��x����F����������ã�S��AOM��S����AEFM�ⷽ�̼��ɵõ������
������A��AE��x����E����M��MF��x����F����������ã�S��AOM��S����AEFM�ⷽ�̼��ɵõ������
��3��������÷����������Ľ���ʽ��Ȼ����P��m��m��������PQΪƽ���ı��εıߺ���PQΪƽ���ı��εĶԽ�����������������ۼ���ȷ����Q�����꣮
��1���ߵ�A��ֱ��y��2x��1�ĵ㣬��A�ĺ�����Ϊ1��
��y��2��1��1��3��
��A��1��3����
�ߵ�A�Ƿ���������y��![]() ��x��0��ͼ���ϵĵ㣬
��x��0��ͼ���ϵĵ㣬
��k��3��
��2����ͼ1�����M��m��![]() ������A��AE��x����E����M��MF��x����F��
������A��AE��x����E����M��MF��x����F��
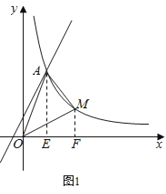
��M��A���Ҳ�ʱ����������ã�S��AOM��S����AEFM��![]() ��3��
��3��![]() ������m1����4��
������m1����4��
��ã�m��3��m=-![]() ����ֵ��ȥ����
����ֵ��ȥ����
��M��A���Ҳ�ʱ����������ã�S��AOM��S����AEFM��![]() ��3��
��3��![]() ������1m����4��
������1m����4��
��ã�m��![]() ��m=-3����ֵ��ȥ����
��m=-3����ֵ��ȥ����
���ϣ�m��3��![]() ��
��
��M��3��1����M��![]() ��9����
��9����
��3���߷���������y��![]() ��x��0��ͼ����A��1��3����
��x��0��ͼ����A��1��3����
��k��1��3��3��
�෴���������Ľ���ʽΪy��![]() ��
��
�ߵ�P��ֱ��y��x�ϣ�
����P��m��m��
����PQΪƽ���ı��εıߣ�
�ߵ�A�ĺ�����ȵ�B�ĺ�����С2����A��������ȵ�B���������2��
���Q�ڵ�P���·������Q������Ϊ��m��2��m2����ͼ2��
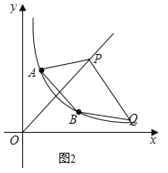
����Q�ڵ�P���Ϸ������Q������Ϊ��m2��m��2����ͼ3��
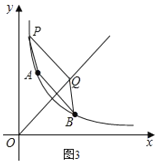
��Q��m��2��m2�����뷴���������Ľ���ʽ�ã���m��2����m-2��=3
m����![]() ��
��
��m��0��
��m��![]() ��
��
��Q1��![]() ��2��
��2��![]() 2����
2����
ͬ���ɵ���һ��Q2��![]() 2��
2��![]() ��2����
��2����
����PQΪƽ���ı��εĶԽ��ߣ���ͼ4��

��A��B����y��x�Գƣ�
��OP��AB
��ʱ��Q��ֱ��y��x�ϣ���Ϊֱ��y��x��˫����y��![]() �Ľ��㣬
�Ľ��㣬
��![]() ���
���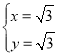 ��
��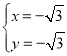 ����ȥ��
����ȥ��
��Q3��![]() ��
��![]() ��
��
�������������������ĵ�Q������������ֱ�Ϊ��Q1��![]() ��2��
��2��![]() 2����Q2��
2����Q2��![]() 2��
2��![]() ��2����Q3��
��2����Q3��![]() ��
��![]() ����
����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵȱ���ABC����һ��D��AD=5��BD=6��CD=4������ABD��A����ʱ����ת��ʹAB��AC�غϣ���D��ת����E������CDE������ֵΪ �� ��
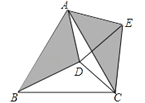
A. ![]() B. 2
B. 2![]() C. 3
C. 3![]() D. 4
D. 4![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���涨��sin����x��=��sinx��cos����x��=cosx��sin��x+y��=sinxcosy+cosxsiny��
�ݴ��ж����е�ʽ�������� ��д��������ȷ����ţ�
��cos����60����=��![]() ��
��
��sin75��=![]() ��
��
��sin2x=2sinxcosx��
��sin��x��y��=sinxcosy��cosxsiny��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=90�㣬AC=6��BC=8������ABC��AB���ϵĵ�D˳ʱ����ת����ת��Ϊ����0��������180�㣩���õ�Rt��A��DE��A��C�佻AB�ڵ�E����AD=BE����AD�ij�Ϊ_____

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
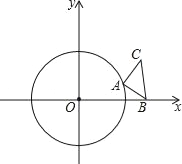
����Ŀ����ͼ����O�İ뾶Ϊ1������ֱ��������ABC�Ķ���B������Ϊ��![]() ��0������CAB=90�㣬AC=AB������A����O���˶���
��0������CAB=90�㣬AC=AB������A����O���˶���
��1������A��x�����������ʱ��ֱ��д����C�����ꣻ
��2������A�˶���x��ĸ�������ʱ�����ж�ֱ��BC����Oλ�ù�ϵ����˵�����ɣ�
��3�����A�ĺ�����Ϊx����ABC�����ΪS����S��x֮��ĺ�����ϵʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��ͼ������һ��������ֱ����ʻ�����У�����������صľ��� s��ǧ�ף�����ʻʱ�� t��Сʱ��֮��ĺ�����ϵ�������ͼ���ṩ����Ϣ������������⣺
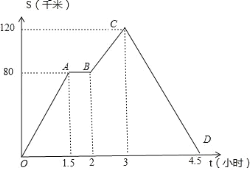
��1�������� OA ����ʻ��ƽ���ٶ���_____km/h���� BC ����ʻ��ƽ���ٶ���_____km/h���� CD ����ʻ��ƽ���ٶ���_____km/h��
��2��AB �α�ʾ�ĺ�����_____��
��3������ȫ������·����_____km��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ʶ����ǿ���̻����������������½���������2014�������̻�����20���䣬��2016���̻�����������Ϊ9.8���䣮�������2014�굽 2016���̻�������������ƽ���½��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������AOBC�ı�OB��OA�ֱ���x��y���ϣ���C����Ϊ��8��8������������AOBC�Ƶ�A��ʱ����ת�Ƕ�����0��������90�������õ�������ADEF��ED���߶�BC�ڵ�Q��ED���ӳ��߽��߶�OB�ڵ�P������AP��AQ��
��1����֤����ACQ�ա�ADQ��
��2�����PAQ�Ķ��������ж��߶�OP��PQ��CQ֮���������ϵ����˵�����ɣ�
��3������BE��EC��CD��DB�õ��ı���BECD������ת�����У��ı���BECD�ܷ��Ǿ��Σ�����ܣ��������P�����꣬������ܣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AB��8��BC��4����������AC�۵�����D���ڵ�D���������ص����֡�AFC�����Ϊ�� ��

A.6B.8C.10D.12
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com