
【题目】如图,在平面直角坐标系中有一直角三角形AOB,O为坐标原点,OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC,抛物线y=ax2+bx+c经过点A、B、C.
(1)求抛物线的解析式;
(2)若点P是第二象限内抛物线上的动点,其横坐标为t,设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求以C、E、F为顶点三角形与△COD相似时点P的坐标.
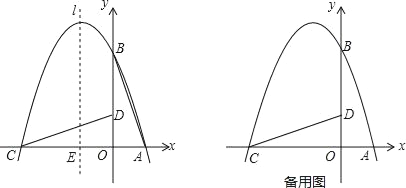
【答案】(1)抛物线的解析式为y=﹣x2﹣2x+3;(2)当△CEF与△COD相似时,P点的坐标为(﹣1,4)或(﹣2,3).
【解析】
(1)根据正切函数,可得OB,根据旋转的性质,可得△DOC≌△AOB,根据待定系数法,可得函数解析式;
(2)分两种情况讨论:①当∠CEF=90°时,△CEF∽△COD,此时点P在对称轴上,即点P为抛物线的顶点;②当∠CFE=90°时,△CFE∽△COD,过点P作PM⊥x轴于M点,得到△EFC∽△EMP,根据相似三角形的性质,可得PM与ME的关系,解方程,可得t的值,根据自变量与函数值的对应关系,可得答案.
(1)在Rt△AOB中,OA=1,tan∠BAO![]() 3,∴OB=3OA=3.
3,∴OB=3OA=3.
∵△DOC是由△AOB绕点O逆时针旋转90°而得到的,∴△DOC≌△AOB,∴OC=OB=3,OD=OA=1,∴A,B,C的坐标分别为(1,0),(0,3),(﹣3,0),代入解析式为
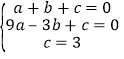 ,解得:
,解得: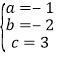 ,抛物线的解析式为y=﹣x2﹣2x+3;
,抛物线的解析式为y=﹣x2﹣2x+3;
(2)∵抛物线的解析式为y=﹣x2﹣2x+3,∴对称轴为l![]() 1,∴E点坐标为(﹣1,0),如图,分两种情况讨论:
1,∴E点坐标为(﹣1,0),如图,分两种情况讨论:
①当∠CEF=90°时,△CEF∽△COD,此时点P在对称轴上,即点P为抛物线的顶点,P(﹣1,4);
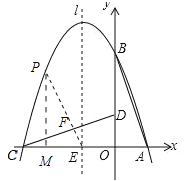
②当∠CFE=90°时,△CFE∽△COD,过点P作PM⊥x轴于M点,∵∠CFE=∠PME=90°,∠CEF=∠PEM,∴△EFC∽△EMP,∴![]() ,∴MP=3ME.
,∴MP=3ME.
∵点P的横坐标为t,∴P(t,﹣t2﹣2t+3).
∵P在第二象限,∴PM=﹣t2﹣2t+3,ME=﹣1﹣t,t<0,∴﹣t2﹣2t+3=3(﹣1﹣t),解得:t1=﹣2,t2=3(与t<0矛盾,舍去).
当t=﹣2时,y=﹣(﹣2)2﹣2×(﹣2)+3=3,∴P(﹣2,3).
综上所述:当△CEF与△COD相似时,P点的坐标为(﹣1,4)或(﹣2,3).


科目:初中数学 来源: 题型:
【题目】一根长18cm的牙刷置于底面直径为5cm、高为12cm的圆柱形水杯中,牙刷露在杯子外面的长度为hcm,则h的取值范围是( )
A. 5cm<h≤6cm B. 6cm<h≤7cm C. 5cm≤h≤6cm D. 5cm≤h<6cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某中学准备围建一个矩形苗圃,其中一边靠墙,另外三边用长为![]() 米的篱笆围成,若墙长为
米的篱笆围成,若墙长为![]() 米,设这个苗圃垂直于墙的一边长为
米,设这个苗圃垂直于墙的一边长为![]() 米.
米.

![]() 若苗圃园的面积为
若苗圃园的面积为![]() 平方米,求
平方米,求![]() 的值;
的值;
![]() 若平行于墙的一边长不小于
若平行于墙的一边长不小于![]() 米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值,如果没有,请说明理由.
米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值,如果没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以圆O为圆心,半径为1的弧交坐标轴于A,B两点,P是弧![]() 上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是
上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是

A. (sinα,sinα) B. (cosα,cosα) C. (cosα,sinα) D. (sinα,cosα)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:sin(﹣x)=﹣sinx,cos(﹣x)=cosx,sin(x+y)=sinxcosy+cosxsiny.
据此判断下列等式成立的是 (写出所有正确的序号)
①cos(﹣60°)=﹣![]() ;
;
②sin75°=![]() ;
;
③sin2x=2sinxcosx;
④sin(x﹣y)=sinxcosy﹣cosxsiny.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】哈市某专卖店销售某品牌服装,该服装进价为每件80元,当每件服装售价为240元时,月销售量为200件,该专卖店为提高经营利润,准备采取降价的方式进行促销,经市场调查发现,当销售单价每降价10元,月销量就增加20件.设每件服装售价为x元,该专卖店的月销售量为y件.
(1)求y与x的关系式;
(2)在某月进货时,该专卖店进货款不超过18000元,售价定为多少元可使月利润达到33000元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,把△ABC绕AB边上的点D顺时针旋转,旋转角为α(0°<α<180°),得到Rt△A′DE,A′C′交AB于点E,若AD=BE,则AD的长为_____

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的图象描述一辆汽车在直线行驶过程中,汽车离出发地的距离 s(千米)和行驶时间 t(小时)之间的函数关系.请根据图中提供的信息,完成下列问题:
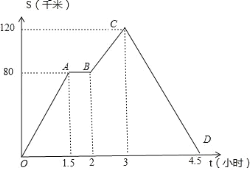
(1)汽车在 OA 段行驶的平均速度是_____km/h,在 BC 段行驶的平均速度是_____km/h,在 CD 段行驶的平均速度是_____km/h.
(2)AB 段表示的含义是_____.
(3)汽车全程所走路程是_____km.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某消防队在一居民楼前进行演习,消防员利用云梯成功救出点B处的求救者后,又发现点B正上方点C处还有一名求救者.在消防车上点A处测得点B和点C的仰角分别是45°和65°,点A距地面2.5米,点B距地面10.5米.为救出点C处的求救者,云梯需要继续上升的高度BC约为多少米?(结果保留整数.参考数据:tan65°≈2.1,sin65°≈0.9,cos65°≈0.4,![]() ≈1.4)
≈1.4)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com