
【题目】将连续奇数1,3,5,7,9,……排成如下的数表:
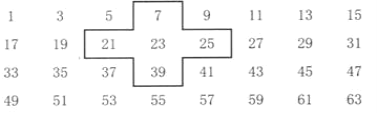
……………
(1)设中间的数为a,求这十字框中五个数之和(请用含字母a的代数式表示);
(2)将十字框上、下、左、右平移,可框住另外五个数,这五个数还有这种规律吗?
(3)十字框中的五个数的和能等于2015吗?若能,请求出这五个数;若不能,说明理由。那么2012呢?
【答案】(1)5a;(2)有;(3)能,387、401、403、405、419;不能,5a![]() 2012.
2012.
【解析】
(1)根据框中的五个数的关系(竖着相邻两数差16,横着相邻两数差2),分别用a表示出其它的四个数,求和即可;
(2)假设中间数为x,再利用(1)的求法说明规律仍然成立即可;
(3)由(2)中得到的规律,利用五个数的和列方程,若能求出奇数a,则能,并求出这五个数即可;若求出的a不是奇数,则不能.
解:(1)根据题意:中间的数为a,则上边的数为(a-16),左边的数为(a-2),右边的数为(a+2),下边的数为(a+16),五个数的和为:
(a-16)+(a-2)+a+(a+2)+(a+16)=5a
(2)有,理由如下:
设中间数为x,则上边的数为(x-16),左边的数为(x-2),右边的数为(x+2),下边的数为(x+16),五个数的和为:
(x-16)+(x-2)+x+(x+2)+(x+16)=5x,故可得结论:十字框中的五个数的和恒等于中间数的5倍.
(3)由(2)中的结论,若十字框中的五个数的和等于2015
5a=2015
解得:a=403,符合题意
则这五个数分别是:387、401、403、405、419;
若十字框中的五个数的和等于2012
5a=2012
a=402.4,不符合题意,故不能.


科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为
表示的数为![]() ,点
,点![]() 到点
到点![]() ,点
,点![]() 的距离相等,动点
的距离相等,动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿数轴向右匀速运动,设运动的时间为
个单位长度的速度沿数轴向右匀速运动,设运动的时间为![]() (
(![]() )秒.
)秒.

(1)点![]() 表示的数是 .
表示的数是 .
(2)点![]() 表示的数是 .(用含有
表示的数是 .(用含有![]() 的代数式表示);
的代数式表示);
(3)求当![]() 等于多少秒时,点
等于多少秒时,点![]() 与点
与点![]() 之间的距离为
之间的距离为![]() 个单位长度.
个单位长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上有两点A、B,它们对应的数分别为a、b,其中a=12.
![]()
(1)在点B的左侧作线段BC=AB,在B的右侧作线段BD=3AB(要求:作出图形,不写作法,保留作图痕迹);
(2)若点C对应的数为c,点D对应的数为的d,且AB=20,求c、d的值;
(3)在(2)的条件下,设点M是BD的中点,N是数轴上一点,且CN=2DN,请直接写出MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若用点A,B,C分别表示有理数a,b,c,它们在数轴上的位置如图所示.
![]()
(1)比较a,b,c的大小(用“<”连接);
(2)请在横线上填上>,< 或 =:a+b____ 0 , b-c____ 0;
(3)化简:2c+|a+b|+|c-b|-|c-a|.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆的周长为4个单位长,数轴每个数字之间的距离为1个单位,在圆的四等分点处分别标上0,1,2,3,先让圆周上表示数字0的点与数轴上表示-1的点重合.再将数轴按逆时针方向环绕在该圆上(如圆周上表示的数字3的点与数轴上表示-2的点重合……),则该数轴上表示-2019的点与圆周上重合的点表示的数字是( )
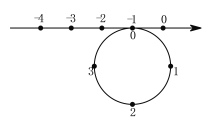
A.0B.1C.2D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.
(1)如图1,连接AF、CE.求证四边形AFCE为菱形,并求AF的长;
(2)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,
①已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.
②若点P、Q的运动路程分别为a、b(单位:cm,ab≠0),已知A、C、P、Q四点为顶点的四边形是平行四边形,求a与b满足的数量关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点F在边BC上,且AF=AD,过点D作DE⊥AF,垂足为点E。
(1)求证:DE=AB;
(2)以D为圆心,DE为半径作圆弧交AD于点G,若BF=FC=1,试求![]() 的长。
的长。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com