
【题目】已知:如图,点E、F、G、H分别在菱形ABCD的各边上,且AE=AH=CF=CG.
(1)求证:四边形EFGH是矩形;
(2)若AB=6,∠A=60°.
①设BE=x,四边形EFGH的面积为S,求S与x之间的函数表达式;
②x为何值时,四边形EFGH的面积S最大?并求S的最大值.

【答案】(1)证明见解析(2)①![]() ②当
②当![]() 时,四边形的面积最大为
时,四边形的面积最大为![]()
【解析】分析:(1)、首先利用菱形的性质得到∠A=∠C,∠B=∠D,AB=BC=CD=DA,然后根据AE=AH=CF=CG,得到BE=BF=DH=DG,从而证得△AEH≌△CGF,△BEF≌△DGH,证得四边形EFGH是平行四边形,然后利用有一个角是直角的平行四边形是矩形判定四边形EFGH是矩形;(2)、①过点B作BN⊥EF于点N,根据题意得出NE和EF的长度,然后根据∠A=60°,AE=AH得出△AEH为等边三角形,从而得出函数关系式;②根据二次函数的性质求出面积的最大值.
详解:(1)、∵四边形ABCD是菱形, ∴![]() .
.
∵![]() , ∴
, ∴![]() . ∴
. ∴![]() . 同理:
. 同理:![]() .
.
所以四边形![]() 是平行四边形. 又∵
是平行四边形. 又∵![]() , ∴
, ∴![]() .
.
∴![]() . ∵
. ∵![]() , ∴
, ∴![]() .
.
∵![]() ,
,
∴![]() . ∴
. ∴![]() . ∴
. ∴![]() .
.
∴四边形![]() 是矩形.
是矩形.
(2)、①过点B作BN⊥EF于点N,根据题意可得:NE=![]() . ∴
. ∴![]() ,∵
,∵![]() ,
,
∴![]() 是等边三角形. ∴
是等边三角形. ∴![]() , ∴
, ∴![]() .
.
②![]() . 当
. 当![]() 时,
时,![]() .
.
所以当![]() 时,四边形的面积最大为
时,四边形的面积最大为![]() .
.
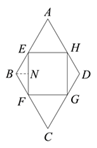


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AH⊥BC,BF平分∠ABC,BE⊥BF,EF∥BC,以下四个结论①AH⊥EF,②∠ABF=∠EFB,③AC∥BE,④∠E=∠ABE.正确的是( )

A. ①②③④ B. ①② C. ①③④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
如图,在平面直角坐标系中,直线y=![]() x-3与坐标轴交于A,B两点.
x-3与坐标轴交于A,B两点.
(1)求A,B两点的坐标;
(2)以AB为边在第四象限内作等边三角形ABC,求△ABC的面积;
(3)在平面内是否存在点M,使得以M,O,A,B为顶点的四边形是平行四边形,若存在,直接写出M点的坐标:若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图是昌平区2019年1月份每天的最低和最高气温,观察此图,下列说法正确的是( )

A.在1月份中,最高气温为10℃,最低气温为-2℃
B.在10号至16号的气温中,每天温差最小为7℃
C.每天的最高气温均高于0℃,最低气温均低于0℃
D.每天的最高气温与最低气温都是具有相反意义的量
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家的洗手盆上装有一种抬启式水龙头(如图1),完全开启后,把手AM的仰角α=37°,此时把手端点A、出水口B和点落水点C在同一直线上,洗手盆及水龙头的相关数据如图2.(参考数据:sin37°=![]() ,cos37°=
,cos37°=![]() ,tan37°=
,tan37°=![]() )
)
求把手端点A到BD的距离;
求CH的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,梯形ABCD中,AB//CD,且AB=2CD,E,F分别是AB,BC的中点.
EF与BD相交于点M.

(1)求证:△EDM∽△FBM;
(2)若DB=9,求BM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,弧AB=弧AC,AP是⊙O的切线,交BO的延长线于点P
(1) 求证:AP∥BC
(2) 若tan∠P=![]() ,求tan∠PAC的值
,求tan∠PAC的值

查看答案和解析>>
科目:初中数学 来源: 题型:
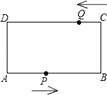
【题目】如图,在矩形ABCD中,AB=24厘米,BC=10厘米,点P从A开始沿AB边以4厘米/秒的速度运动,点Q从C开始沿CD边2厘米/秒的速度移动,如果点P、Q分别从A、C同时出发,当其中一点到达终点时,另一点也随之停止运动,设运动时间为t秒.
(1)当t=2秒时,求P、Q两点之间的距离;
(2)t为何值时,线段AQ与DP互相平分?
(3)t为何值时,四边形APQD的面积为矩形面积的![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直角三角形ABC中,∠C=90°,将△ABC绕点A逆时针旋转至△AED,使点C的对应点D恰好落在边AB上,E为点B的对应点.设∠BAC=α,则∠BED=______.(用含α的代数式表示)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com