
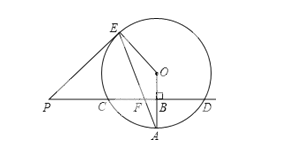
【题目】已知直线PD垂直平分⊙O的半径OA于点B,PD交⊙O于点C、D,PE是⊙O的切线,E为切点,连结AE,交CD于点F.
(1)若⊙O的半径为8,求CD的长;
(2)证明:PE=PF;
【答案】(1)、CD=8![]() ;(2)、证明过程见解析.
;(2)、证明过程见解析.
【解析】
试题分析:(1)、连接OD,根据垂径定理可得:OB=4,OD=8,根据Rt△OBD的勾股定理求出BD的长度,然后求出CD的长度;(2)、根据切线性质可得∠PEO=90°,根据OA=OE得出∠A=∠AEO,根据∠PEF=90°-∠AEO,∠PFE=∠AFB=90°-∠A得出∠PEF=∠PFE,从而得出PE=PF.
试题解析:(1)、连接OD,∵直线PD垂直平分⊙O的半径OA于点B,⊙O的半径为8,
∴OB=![]() OA=4,BC=BD=
OA=4,BC=BD=![]() CD, ∴在Rt△OBD中,BD=
CD, ∴在Rt△OBD中,BD=![]() =4
=4![]() , ∴CD=2BD=8
, ∴CD=2BD=8![]() ;
;
(2)、∵PE是⊙O的切线, ∴∠PEO=90°,
∴∠PEF=90°﹣∠AEO,∠PFE=∠AFB=90°﹣∠A,
∵OE=OA, ∴∠A=∠AEO, ∴∠PEF=∠PFE, ∴PE=PF;


科目:初中数学 来源: 题型:
【题目】下列命题是真命题的是( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.对角线互相垂直的平行四边形是矩形
C.四条边相等的四边形是菱形
D.正方形是轴对称图形,但不是中心对称图形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图所示,B、C、D三点在同一条直线上,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )
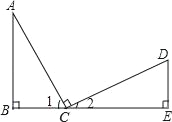
A. ∠A与∠D互为余角 B. ∠A=∠2 C. △ABC≌△ CED D. ∠1=∠2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种饮料,每瓶进价为4元.经市场调查表明,当售价在5元到8元之间(含5元,8元)浮动时,每瓶售价每增加1元,日均销售量减少40瓶;当售价为每瓶为6元时,日均销售量为120瓶.问:销售价格定为每瓶多少元时,所得日均毛利润(每瓶毛利润=每瓶售价-每瓶进价)最大?最大日均毛利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
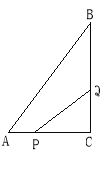
【题目】如图所示,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从C点出发沿CB边向点B以2cm/s的速度移动.
(1)如果P、Q同时出发,几秒钟后,可使△PCQ的面积为8平方厘米?
(2)点P、Q在移动过程中,是否存在某一时刻,使得△PCQ的面积等于△ABC的面积的一半.若存在,求出运动的时间;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
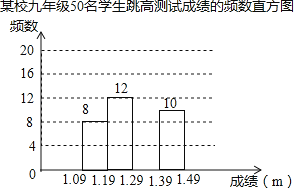
【题目】为了了解某校九年级学生的跳高水平,随机抽取该年级50名学生进行跳高测试,并把测试成绩绘制成如图所示的频数表和未完成的频数直方图(每组含前一个边界值,不含后一个边界值).
某校九年级50名学生跳高测试成绩的频数表
组别(m) | 频数 |
1.09~1.19 | 8 |
1.19~1.29 | 12 |
1.29~1.39 | A |
1.39~1.49 | 10 |
(1)求a的值,并把频数直方图补充完整;
(2)该年级共有500名学生,估计该年级学生跳高成绩在1.29m(含1.29m)以上的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,由长度为1个单位的若干小正方形组成的网格图中,点A、B、C在小正方形的顶点上.
(1)在图中画出与△ABC关于直线l成轴对称的△AB′C′;
(2)三角形ABC的面积为
(3)以AC为边作与△ABC全等的三角形(只要作出一个符合条件的三角形即可);
(4)在直线l上找一点P,使PB+PC的长最短.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com