
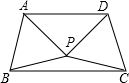
 如图,△ABP与△CDP是两个全等的等边三角形,且PA⊥PD,下列四个结论:
如图,△ABP与△CDP是两个全等的等边三角形,且PA⊥PD,下列四个结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 先求出∠BPC的度数,再根据对称性得到△BPC为等腰三角形,∠PCB的度数即可求出;再根据题意,有△APD是等腰直角三角形;△PBC是等腰三角形;结合轴对称图形的定义与判定,可得四边形ABCD是轴对称图形,进而可得正确结论.
解答 解:∵△ABP≌△CDP,
∴AB=CD,AP=DP,BP=CP.
又∵△ABP与△CDP是两个等边三角形,
∴∠PAB=∠PBA=∠APB=60°.
①根据题意,∠BPC=360°-60°×2-90°=150°
∵BP=PC,
∴∠PCB=(180°-150°)÷2=15°,故本选项正确;
②∵∠ABC=60°+15°=75°,
∵AP=DP,
∴∠DAP=45°,
∵∠BAP=60°,
∴∠BAD=∠BAP+∠DAP=60°+45°=105°,
∴∠BAD+∠ABC=105°+75°=180°,
∴AD∥BC,故本选项正确;
③延长CP交于AB于点O.
∠APO=180°-(∠APD+∠CPD)=180°-(90°+60°)=180°-150°=30°,
∵∠PAB=60°,
∴∠AOP=30°+60°=90°,
即PC⊥AB,故本选项正确;
④根据题意可得四边形ABCD是轴对称图形,故本选项正确.
综上所述,以上四个结论都正确.
故选D.
点评 本题考查全等三角形的判定与性质以及轴对称图形的定义与判定的综合应用,如果一个图形沿着一条直线对折,两侧的图形能完全重合,这个图形就是轴对称图形,折痕所在的这条直线叫做对称轴.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案科目:初中数学 来源: 题型:选择题
 二次函数y=ax2+bx+c的图象如图所示,则一次函数y=ax+b与反比例函数y=$\frac{c}{x}$在同一平面坐标系中的图象可能是( )
二次函数y=ax2+bx+c的图象如图所示,则一次函数y=ax+b与反比例函数y=$\frac{c}{x}$在同一平面坐标系中的图象可能是( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 学生 | 小红 | 小刚 | 小敏 | 小明 |
| 平均数 | 136 | 136 | 136 | 136 |
| 方差 | 0.32 | 0.18 | 0.24 | 0.27 |
| A. | 小红 | B. | 小刚 | C. | 小敏 | D. | 小明 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com