
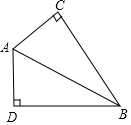
 如图,∠C=∠D=90°,AC=AD,那么△ABC与△ABD全等的理由是( )
如图,∠C=∠D=90°,AC=AD,那么△ABC与△ABD全等的理由是( )| A. | HL | B. | SAS | C. | ASA | D. | AAS |
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 3 | C. | 7 | D. | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 平行四边形ABCD在平面直角坐标系中的位置如图所示,其中A(-6,0),B(4,0),C(5,3),反比例函数y=$\frac{k}{x}$的图象经过点C.
平行四边形ABCD在平面直角坐标系中的位置如图所示,其中A(-6,0),B(4,0),C(5,3),反比例函数y=$\frac{k}{x}$的图象经过点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一位旅行者在早晨8时从城市出发到乡村,第一个小时走了5千米,然后他上坡,1个小时只走了3千米,以后就休息;休息后平均每小时走4千米,在中午12时到达乡村.根据下图回答问题:
一位旅行者在早晨8时从城市出发到乡村,第一个小时走了5千米,然后他上坡,1个小时只走了3千米,以后就休息;休息后平均每小时走4千米,在中午12时到达乡村.根据下图回答问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com