
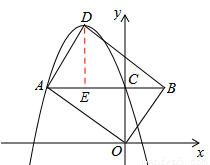
��ͼ����֪��ƽ��ֱ������ϵxOy�У�O������ԭ�㣬������y=��x2+bx+c��c��0���Ķ���ΪD����y��Ľ���ΪC������C��CA��x�ύ�������ڵ�A����AC�ӳ�����ȡ��B��ʹBC= AC������OA��OB��BD��AD��
AC������OA��OB��BD��AD��
��1������A�������ǣ���4��4��
����b��c��ֵ��
�����ж��ı���AOBD����״����˵�����ɣ�
��2���Ƿ���������ĵ�A��ʹ���ı���AOBD�Ǿ��Σ������ڣ���ֱ��д��һ�����������ĵ�A�����ꣻ�������ڣ���˵�����ɣ�

��1����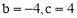 �����ı���AOBD��ƽ���ı��Σ���������������2�����ڣ���A����������ǣ�
�����ı���AOBD��ƽ���ı��Σ���������������2�����ڣ���A����������ǣ�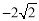 ��2����
��2����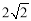 ��2��.
��2��.
��������
�����������1�������������ϵĵ��������������������b��c��ֵ.
����֤AD=BO��AD��BO�����ж��ı���Ϊƽ���ı���.
��2��Ҫʹ�ı���AOBD�Ǿ��Σ�������AOB=��BCO=90�㣬
�ߡ�ABO=��OBC�����ABO�ס�OBC. �� ��
��
����AB=AC+BC=3BC����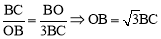 .
.
����Rt��OBC�У����ݹ��ɶ����ɵã�OC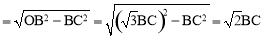 .
.
��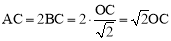 .
.
��C������������y�ύ�㣬��OC=c.
��A��������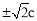 ��c���������������
��c���������������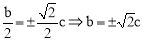 .
.
��A�����y=��x2+bx+c�ɵ�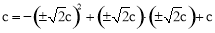 �����
�����
��������Ϊ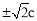 ��������Ϊc���ɣ���c=2��
��������Ϊc���ɣ���c=2��
��A�����������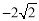 ��2����
��2����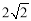 ��2��.
��2��.
�����������������
��1���١�AC��x�ᣬA������Ϊ����4��4��������C�������ǣ�0��4��
��A��C����y�T��x2+bx+c���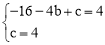 �����
�����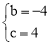 .
.
���ı���AOBD��ƽ���ı��Σ��������£�
�����������ߵĽ���ʽΪ ��
��
��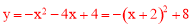 ��������D����������2��8��.
��������D����������2��8��.
���ͼ������D����DE��AB�ڵ�E����DE=OC=4��AE=2��
��AC=4��BC= AC����BC=
AC����BC= AC=2. ��AE=BC��
AC=2. ��AE=BC��
��AC��x�ᣬ���AED=��BCO=90��.
���AED�ա�BCO����AD=BO����DAE=��BCO. ��AD��BO.���ı���AOBD��ƽ���ı��Σ�
��2�����ڣ���A����������ǣ�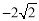 ��2����
��2����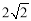 ��2��.
��2��.
���㣺1.���κ����ۺ��⣻2.�����ϵ�������뷽�̵Ĺ�ϵ��3.���κ��������ʣ�4.ƽ���ı��ε��ж������ʣ�5.ȫ�������ε��ж������ʣ�6.���������ε��ж������ʣ�7.���ɶ�����8.���ε����ʣ�


 ��ѧ�̸̳����¿α�ϵ�д�
��ѧ�̸̳����¿α�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ������人������ѧ�������棩 ���ͣ������
����װ�д�С��ͬ��2�������2������
��1���ȴӴ�������1�����Żأ���Ͼ��Ⱥ�������1����
�� ���һ���������ڶ�����������ĸ��ʣ�
�� ������������������1�������1������ĸ��ʣ�
��2���ȴӴ�������1����Żأ�������1����������������������1�������1������ĸ����Ƕ��٣���ֱ��д�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ������˲�������ѧ�������棩 ���ͣ�ѡ����
��ҵʱ������Сѧ���������ۺ�����ָ��Ŀ���Ҫ��֮һ���ڷ�ѧϰС�����ͬѧÿ�������ҵʱ��ֱ��ǣ���λ�����ӣ���60��80��75��45��120���������ݵ���λ������ ��
A. 45 B. 75 C. 80 D. 60
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��㽭��ɽ������ѧ�������棩 ���ͣ�ѡ����
С��ͬѧ���Լ�5�·ݵĸ��������������������ͳ��ͼ(��ͼ)����ͼ�пɿ����� ��
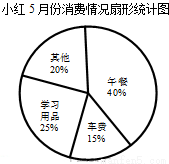
(A)�������ѽ��ռ�����ܽ��İٷֱ�
(B)�������ѵĽ��
(C)���ѵ��ܽ��
(D)�������ѽ��������仯���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��㽭���ݾ�����ѧ�������棩 ���ͣ������
����2x��1=0�Ľ���x= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��㽭���ݾ�����ѧ�������棩 ���ͣ������
��ͼ������������ֽ�У�ÿ��С�����α߳�����1�����Ϊ���������������������ξ�Ϊ��������Σ������ڷ��㴦��.�밴Ҫ��ͼ�ס�ͼ���е�ָ��ͼ�ηָ�����������Σ�ʹ��������Ϊ���������������������ηֱ��Ӧȫ��.
��1��ͼ���еĸ��������ABCD��
��2��ͼ���е�ƽ���ı���ABCD.
ע��ͼ�ס�ͼ���ڴ���ϣ��ָ�����ʵ��.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��㽭����������ѧ�������棩 ���ͣ������
ľ����ʦ���ó�AB=3����BC=2�ľ���ľ����һ�������ܴ��Բ�����棬����������ַ�����
����һ��ֱ�Ӿ�һ���뾶����Բ��
��������Բ��O1��O2�ֱ���CD��AB�ϣ��뾶�ֱ���O1C��O2A�����������еİ�Բƴ��һ��Բ��
���������ضԽ���AC�����ξ�����������Σ��ʵ�ƽ�������β���һ������Բ��
�����ģ���һ��С����BCEFƴ�ӵ�����AEFD���棬������ƴ�ɵ�ľ���һ�������ܴ��Բ��
��1��д������һ�е�Բ�İ뾶��
��2��ͨ������˵���������ͷ������У��ĸ�Բ�İ뾶�ϴ�
��3���ڷ������У���CE= ��
�� ����Բ�İ뾶Ϊ
����Բ�İ뾶Ϊ ��
��
���� ����
���� �ĺ�������ʽ��
�ĺ�������ʽ��
�ڵ� ȡ��ֵʱԲ�İ뾶������뾶�Ƕ��٣���˵�����ַ����У���һ��Բ������İ뾶���
ȡ��ֵʱԲ�İ뾶������뾶�Ƕ��٣���˵�����ַ����У���һ��Բ������İ뾶���

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com