
ľ����ʦ���ó�AB=3����BC=2�ľ���ľ����һ�������ܴ��Բ�����棬����������ַ�����
����һ��ֱ�Ӿ�һ���뾶����Բ��
��������Բ��O1��O2�ֱ���CD��AB�ϣ��뾶�ֱ���O1C��O2A�����������еİ�Բƴ��һ��Բ��
���������ضԽ���AC�����ξ�����������Σ��ʵ�ƽ�������β���һ������Բ��
�����ģ���һ��С����BCEFƴ�ӵ�����AEFD���棬������ƴ�ɵ�ľ���һ�������ܴ��Բ��
��1��д������һ�е�Բ�İ뾶��
��2��ͨ������˵���������ͷ������У��ĸ�Բ�İ뾶�ϴ�
��3���ڷ������У���CE= ��
�� ����Բ�İ뾶Ϊ
����Բ�İ뾶Ϊ ��
��
���� ����
���� �ĺ�������ʽ��
�ĺ�������ʽ��
�ڵ� ȡ��ֵʱԲ�İ뾶������뾶�Ƕ��٣���˵�����ַ����У���һ��Բ������İ뾶���
ȡ��ֵʱԲ�İ뾶������뾶�Ƕ��٣���˵�����ַ����У���һ��Բ������İ뾶���

����������һ��Բ�İ뾶Ϊ��
��������������Բ�뾶�ϴ�
(3) �ٵ�0<x< ʱ��y=
ʱ��y=
�� ʱ��
ʱ��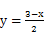
�ڵ� ʱ��y���y���=
ʱ��y���y���= ��
��
���ַ����У������ַ���Բ������İ뾶���
��������
�����������1��Բ��ֱ������BC�ij�
�����������������������ţ����ͣ����ڣţ�Ȼ�����ù��ɶ������ɵ�
�����������ϣǣ�Ȼ�����á��ϣãǡס��ãģż��ɵ�
��3����������ۣ���0<x< ��
�� ��������������
��������������
�������������������һ��Բ�İ뾶Ϊ��
������������
��ͼ�����������������ţ����ͣ����ڣţ�������ţ��أ�

��ô�����أ��������������������أ�������ãأ�
������
���ϣǣ���ϣǡͣãģ��ߡϣģ������㣬��ϣǣ����ģ�
����ϣãǡס��ãģţ���
��ϣǣ������� ,��y=
,��y= ���������Բ�뾶�ϴ�
���������Բ�뾶�ϴ�
(3) �ٵ�0<x< ʱ��y=
ʱ��y=

�� ʱ��
ʱ��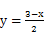
�ڵ� ʱ��y���y���=
ʱ��y���y���= ��
��
���ַ����У������ַ���Բ������İ뾶���
���㣺1����Բ���У�2��Բ�����ߣ�3�����ɶ�����4������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��㽭���ݾ�����ѧ�������棩 ���ͣ������
��ͼ����֪��ƽ��ֱ������ϵxOy�У�O������ԭ�㣬������y=��x2+bx+c��c��0���Ķ���ΪD����y��Ľ���ΪC������C��CA��x�ύ�������ڵ�A����AC�ӳ�����ȡ��B��ʹBC= AC������OA��OB��BD��AD��
AC������OA��OB��BD��AD��
��1������A�������ǣ���4��4��
����b��c��ֵ��
�����ж��ı���AOBD����״����˵�����ɣ�
��2���Ƿ���������ĵ�A��ʹ���ı���AOBD�Ǿ��Σ������ڣ���ֱ��д��һ�����������ĵ�A�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��㽭���ݾ�����ѧ�������棩 ���ͣ�ѡ����
һ�κ��� ��ͼ����y�ύ����������� ��
��ͼ����y�ύ����������� ��
A.��0��-4�� B.��0��4�� C.��2��0�� D.��-2��0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��㽭���ݾ�����ѧ�������棩 ���ͣ������
��ֱ֪�� ������1=40��50�䣬����2= .
������1=40��50�䣬����2= .

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��㽭���ݾ�����ѧ�������棩 ���ͣ�ѡ����
���������У���ȷ������ ��
A .���εĶԽ������ B.���εĶԽ��߲����
C.���εĶԽ��߲��ܻ��ഹֱ D.ƽ���ı��εĶԽ��߿��Ի��ഹֱ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��㽭����������ѧ�������棩 ���ͣ������
��ͼ����A�ص�B�صĹ�·��Ҫ����C�أ�ͼ��AC=10ǧ�ף���CAB=25�㣬��CBA=37�㡣����й滮����Ҫ������A��B����֮����һ����ֱ�Ĺ�·��
��1�����ֱ��Ĺ�·AB�ij���
��2���ʣ���·������ԭ�������˶���ǧ�ף�
��sin25���0.42��cos25���0.91��sin37���0.60��tan37���0.75��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ������ϲ�������ѧ�������棩 ���ͣ������
ͼ1�е��й���Ҽ������ĸ���ͬ�������ڶ��㴦���δ������ɣ�ÿ�����������ξ���30��ļнǣ�ʾ��ͼ��ͼ2����ͼ2�У�ÿ�����εı߳�Ϊ10cm�����Ϊ60�㣮
��1������CD��EB���������ǵ�λ�ù�ϵ������֤����
��2����A��B����֮��ľ��루���ȡ����������ʹ�ü�������
���ο����ݣ� ��1.41��
��1.41�� ��1.73��
��1.73�� ��2.45��
��2.45��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ�����������ѧ�������棩 ���ͣ������
һ�������Ӽ�����ʻ���ҵأ���������˰�Сʱж�����漴���ٷ��أ���֪�������ص��ٶ������Ӽ�ʻ���ҵص��ٶȵ�1.5����������صľ���y��ǧ�ף�����ʱ��x��Сʱ���ĺ���ͼ����ͼ��ʾ����a= ��Сʱ����

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com