
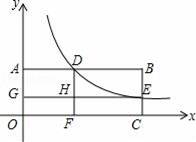
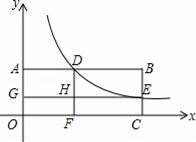
如图,矩形OABC的顶点A在y轴上,C在x轴上,双曲线y=
 与AB交于点D,与BC交于点E,DF⊥x轴于点F,EG⊥y轴于点G,交DF于点H.若矩形OGHF和矩形HDBE的面积分别是1和2,则k的值为( )
与AB交于点D,与BC交于点E,DF⊥x轴于点F,EG⊥y轴于点G,交DF于点H.若矩形OGHF和矩形HDBE的面积分别是1和2,则k的值为( )

A.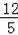
 B.
B.
 +1 C.
+1 C.
 D.2
D.2

B【考点】反比例函数系数k的几何意义.
【专题】计算题.
【分析】设D(t,
 ),由矩形OGHF的面积为1得到HF=
),由矩形OGHF的面积为1得到HF=
 ,于是根据反比例函数图象上点的坐标特征可表示出E点坐标为(kt,
,于是根据反比例函数图象上点的坐标特征可表示出E点坐标为(kt,
 ),接着利用矩形面积公式得到(kt﹣t)•(
),接着利用矩形面积公式得到(kt﹣t)•(
 ﹣
﹣
 )=2,然后解关于k的方程即可得到满足条件的k的值.
)=2,然后解关于k的方程即可得到满足条件的k的值.
【解答】解:设D(t,
 ),
),
∵矩形OGHF的面积为1,DF⊥x轴于点F,
∴HF=
 ,
,
而EG⊥y轴于点G,
∴E点的纵坐标为
 ,
,
当y=
 时,
时,
 =
=
 ,解得x=kt,
,解得x=kt,
∴E(kt,
 ),
),
∵矩形HDBE的面积为2,
∴(kt﹣t)•(
 ﹣
﹣
 )=2,
)=2,
整理得(k﹣1)2=2,
而k>0,
∴k=
 +1.
+1.
故选B.

【点评】本题考查了反比例函数比例系数k的几何意义:在反比例函数y=
 图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.
图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
如图1,已知AB//CD,C在D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E.∠ADC=70°.
(1)则∠EDC的度数为 ;
(2)若∠ABC=n°,求∠BED的度数(用含n的代数式表示);
(3)将线段BC沿DC方向平移,使得点B在点A的右侧,其他条件不变,若∠ABC=n°,求∠BED的度数(用含n的代数式表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
下列说法正确的是( )
①代数式
 的意义是a除以b的商与1的和;
的意义是a除以b的商与1的和;
②要使y=
 有意义,则x应该满足0<x≤3;
有意义,则x应该满足0<x≤3;
③当2x﹣1=0时,整式2xy﹣8x2y+8x3y的值是0;
④地球上的陆地面积约为149000000平方千米,用科学记数法表示为1.49×108平方千米.
A.①④ B.①② C.②③ D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
阅读与思考:
整式乘法与因式分解是方向相反的变形
由(x+p)(x+q)=x2+(p+q)x+pq得,x2+(p+q)x+pq=(x+p)(x+q);
利用这个式子可以将某些二次项系数是1的二次三项式分解因式,
例如:将式子x2+3x+2分解因式.
分析:这个式子的常数项2=1×2,一次项系数3=1+2,所以x2+3x+2=x2+(1+2)x+1×2.
解:x2+3x+2=(x+1)(x+2)
请仿照上面的方法,解答下列问题
(1)分解因式:x2+7x﹣18=
启发应用
(2)利用因式分解法解方程:x2﹣6x+8=0;
(3)填空:若x2+px﹣8可分解为两个一次因式的积,则整数p的所有可能值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,直线y=x+1与y轴交于A点,与反比例函数
 (x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=
(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=
 .
.
(1)求k的值;
(2)设点N(1,a)是反比例函数
 (x>0)图象上的点,在y轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.
(x>0)图象上的点,在y轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com