
【题目】已知![]() ,H为射线OA上一定点,
,H为射线OA上一定点,![]() ,P为射线OB上一点,M为线段OH上一动点,连接PM,满足
,P为射线OB上一点,M为线段OH上一动点,连接PM,满足![]() 为钝角,以点P为中心,将线段PM顺时针旋转
为钝角,以点P为中心,将线段PM顺时针旋转![]() ,得到线段PN,连接ON.
,得到线段PN,连接ON.
(1)依题意补全图1;
(2)求证:![]() ;
;
(3)点M关于点H的对称点为Q,连接QP.写出一个OP的值,使得对于任意的点M总有ON=QP,并证明.

【答案】(1)如图所示见解析;(2)见解析;(3)OP=2.证明见解析.
【解析】
(1)根据题意画出图形即可.
(2)由旋转可得∠MPN=150°,故∠OPN=150°-∠OPM;由∠AOB=30°和三角形内角和180°可得∠OMP=180°-30°-∠OPM=150°-∠OPM,得证.
(3)根据题意画出图形,以ON=QP为已知条件反推OP的长度.由(2)的结论∠OMP=∠OPN联想到其补角相等,又因为旋转有PM=PN,已具备一边一角相等,过点N作NC⊥OB于点C,过点P作PD⊥OA于点D,即可构造出△PDM≌△NCP,进而得PD=NC,DM=CP.此时加上ON=QP,则易证得△OCN≌△QDP,所以OC=QD.再设DM=CP=x,所以OC=OP+PC=2+x,MH=MD+DH=x+1,由于点M、Q关于点H对称,得出DQ=DH+HQ=1+x+1=2+x,得出OC=DQ,再利用SAS得出△OCN≌△QDP即可
解:(1)如图1所示为所求.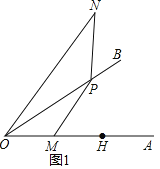
(2)设∠OPM=α,
∵线段PM绕点P顺时针旋转150°得到线段PN
∴∠MPN=150°,PM=PN
∴∠OPN=∠MPN-∠OPM=150°-α
∵∠AOB=30°
∴∠OMP=180°-∠AOB-∠OPM=180°-30°-α=150°-α
∴∠OMP=∠OPN
(3)OP=2时,总有ON=QP,证明如下:
过点N作NC⊥OB于点C,过点P作PD⊥OA于点D,如图2
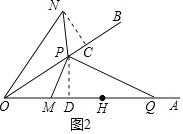
∴∠NCP=∠PDM=∠PDQ=90°
∵∠AOB=30°,OP=2
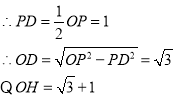
∴DH=OH-OD=1
∵∠OMP=∠OPN
∴180°-∠OMP=180°-∠OPN
即∠PMD=∠NPC
在△PDM与△NCP中
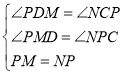
∴△PDM≌△NCP(AAS)
∴PD=NC,DM=CP
设DM=CP=x,则OC=OP+PC=2+x,MH=MD+DH=x+1
∵点M关于点H的对称点为Q
∴HQ=MH=x+1
∴DQ=DH+HQ=1+x+1=2+x
∴OC=DQ
在△OCN与△QDP中
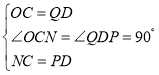
∴△OCN≌△QDP(SAS)
∴ON=QP


科目:初中数学 来源: 题型:
【题目】岳阳市整治农村“空心房”新模式,获评全国改革开放40年地方改革创新40案例.据了解,我市某地区对辖区内“空心房”进行整治,腾退土地1200公顷用于复耕和改造,其中复耕土地面积比改造土地面积多600公顷.
(1)求复耕土地和改造土地面积各为多少公顷;
(2)该地区对需改造的土地进行合理规划,因地制宜建设若干花卉园和休闲小广场,要求休闲小广场总面积不超过花卉园总面积的![]() ,求休闲小广场的总面积最多为多少公顷.
,求休闲小广场的总面积最多为多少公顷.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,抛物线![]() 的顶点坐标为
的顶点坐标为![]() ,并与
,并与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是对称轴与
是对称轴与![]() 轴的交点.
轴的交点.
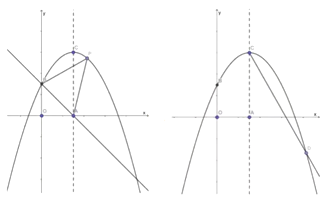
(1)求抛物线的解析式;
(2)如图①所示, ![]() 是抛物线上的一个动点,且位于第一象限,连结BP、AP,求
是抛物线上的一个动点,且位于第一象限,连结BP、AP,求![]() 的面积的最大值;
的面积的最大值;
(3)如图②所示,在对称轴![]() 的右侧作
的右侧作![]() 交抛物线于点
交抛物线于点![]() ,求出
,求出![]() 点的坐标;并探究:在
点的坐标;并探究:在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() ?若存在,求点
?若存在,求点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() .
.
(1)如图1,若点![]() 是直线
是直线![]() 上方抛物线上的一个动点,过点
上方抛物线上的一个动点,过点![]() 作
作![]() 轴交直线
轴交直线![]() 于点
于点![]() ,作
,作![]() 于点
于点![]() ,点
,点![]() 为直线
为直线![]() 上一动点,点
上一动点,点![]() 为
为![]() 轴上一动点,连接
轴上一动点,连接![]() ,
,![]() .当
.当![]() 最长时,求
最长时,求![]() 的最小值;
的最小值;
(2)如图2,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得
得![]() ,将
,将![]() 沿直线
沿直线![]() 平移得到
平移得到![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() ,将
,将![]() 沿边
沿边![]() 翻折得
翻折得![]() ,连接
,连接![]() ,
,![]() ,当
,当![]() 是等腰三角形时,求此时点
是等腰三角形时,求此时点![]() 的坐标.
的坐标.
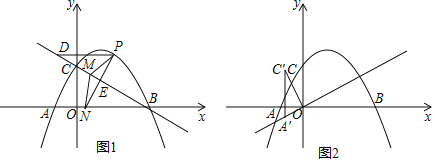
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰Rt△ABC中,∠ABC=90°,点D在AC上,将△ABD绕顶点B沿顺时针方向旋转90°后得到△CBE.
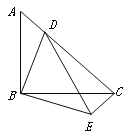
(1)求∠DCE的度数;
(2)当AB=4,AD∶DC=1∶3时,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
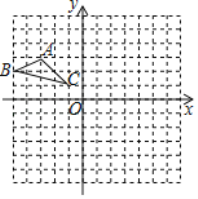
【题目】△ABC在边长为l的正方形网格中如图所示.
①以点C为位似中心,作出△ABC的位似图形△A1B1C,使其位似比为1:2.且△A1B1C位于点C的异侧,并表示出A1的坐标.
②作出△ABC绕点C顺时针旋转90°后的图形△A2B2C.
③在②的条件下求出点B经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
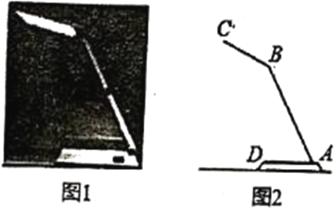
【题目】如图1是一种折叠台灯,将其放置在水平桌面上,图2是其简化示意图,测得其灯臂![]() 长为
长为![]() 灯翠
灯翠![]() 长为
长为![]() ,底座
,底座![]() 厚度为
厚度为![]() 根据使用习惯,灯臂
根据使用习惯,灯臂![]() 的倾斜角
的倾斜角![]() 固定为
固定为![]() ,
,
(1)当![]() 转动到与桌面平行时,求点
转动到与桌面平行时,求点![]() 到桌面的距离;
到桌面的距离;
(2)在使用过程中发现,当![]() 转到至
转到至![]() 时,光线效果最好,求此时灯罩顶端
时,光线效果最好,求此时灯罩顶端![]() 到桌面的高度(参考数据:
到桌面的高度(参考数据:![]() ,结果精确到个位).
,结果精确到个位).
查看答案和解析>>
科目:初中数学 来源: 题型:
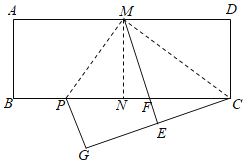
【题目】如图,在矩形ABCD中,AD=2![]() AB.将矩形ABCD对折,得到折痕MN,沿着CM折叠,点D的对应点为E,ME与BC的交点为F;再沿着MP折叠,使得AM与EM重合,折痕为MP,此时点B的对应点为G.下列结论:①△CMP是直角三角形;②AB=
AB.将矩形ABCD对折,得到折痕MN,沿着CM折叠,点D的对应点为E,ME与BC的交点为F;再沿着MP折叠,使得AM与EM重合,折痕为MP,此时点B的对应点为G.下列结论:①△CMP是直角三角形;②AB=![]() BP;③PN=PG;④PM=PF;⑤若连接PE,则△PEG∽△CMD.其中正确的个数为( )
BP;③PN=PG;④PM=PF;⑤若连接PE,则△PEG∽△CMD.其中正确的个数为( )
A.5个B.4个C.3个D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】廊桥是我国古老的文化遗产.如图,是某座抛物线型的廊桥示意图,已知抛物线的函数表达式为![]() ,为保护廊桥的安全,在该抛物线上距水面
,为保护廊桥的安全,在该抛物线上距水面![]() 高为8米的点
高为8米的点![]() 、
、![]() 处要安装两盏警示灯,则这两盏灯的水平距离
处要安装两盏警示灯,则这两盏灯的水平距离![]() 是____米.
是____米.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com