
【题目】如图,在平面直角坐标系中,直线![]() 上一点
上一点![]() ,
,![]() 为
为![]() 轴上一点,连接
轴上一点,连接![]() ,线段
,线段![]() 绕点
绕点![]() 逆时针旋转90°至线段
逆时针旋转90°至线段![]() ,过点
,过点![]() 作直线
作直线![]() 轴,垂足为
轴,垂足为![]() ,直线
,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,且
,且![]() ,连接
,连接![]() ,直线
,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,则点
,则点![]() 的坐标为(______)
的坐标为(______)
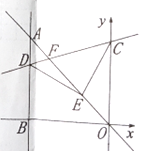
【答案】(![]() ,
,![]() ).
).
【解析】
过E作MN⊥y轴,交y轴于M,交AB于N,过D作DH⊥y轴,交y轴于H,∠CME=∠DNE=∠CED=90°,求出∠MCE=∠DEN,证△MCE≌△NED,推出DN=EM,EN=CM,设AD=a,求出DN=2a1,得出2a1=1,求出a=1,得出D的坐标,在Rt△DNE中,由勾股定理求出EC=ED=![]() ,在Rt△MCE中,由勾股定理求出CM=2,得出C的坐标,设直线CD的解析式是y=kx+3,把D(-3,2)代入求出直线CD的解析式,解由两函数解析式组成的方程组,求出方程组的解即可.
,在Rt△MCE中,由勾股定理求出CM=2,得出C的坐标,设直线CD的解析式是y=kx+3,把D(-3,2)代入求出直线CD的解析式,解由两函数解析式组成的方程组,求出方程组的解即可.
解:过E作MN⊥y轴,交y轴于M,交AB于N,过D作DH⊥y轴,交y轴于H,
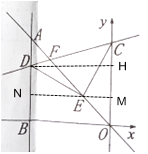
∠CME=∠DNE=∠CED=90°,
∴∠MCE+∠CEM=90°,∠MEC+∠DEN=90°,
∴∠MCE=∠DEN,
∵E(-1,1),
∴OM=BN=1,EM=1,
在△MCE和△NED中,
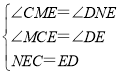
∴△MCE≌△NED(AAS),
∴DN=EM,EN=CM,
∵BD=2AD,
∴设AD=a,BD=2a,
∵E(1,1),
∴BN=2a1,
则2a1=1,
a=1,即BD=2.
∵直线y=-x,
∴AB=OB=3,
在Rt△DNE中,由勾股定理得:EC=ED=![]() ,
,
在Rt△MCE中,由勾股定理得:CM=![]()
则C的坐标是(0,3),
设直线CD的解析式是y=kx+3,
把D(-3,2)代入得:k=![]() ,
,
即直线CD的解析式是y=![]() x+3,
x+3,
即方程组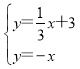
得: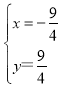
即F的坐标是(![]() ,
,![]() ).
).
故答案为:(![]() ,
,![]() ).
).


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,若点
中,若点![]() 和点
和点![]() 关于
关于![]() 轴对称,点
轴对称,点![]() 和点
和点![]() 关于直线
关于直线![]() 对称,则称点
对称,则称点![]() 是点
是点![]() 关于
关于![]() 轴,直线
轴,直线![]() 的二次对称点.
的二次对称点.
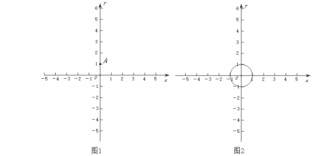
(1)如图1,点![]() .
.
①若点![]() 是点
是点![]() 关于
关于![]() 轴,直线
轴,直线![]() :
:![]() 的二次对称点,则点
的二次对称点,则点![]() 的坐标为________;
的坐标为________;
②若点![]() 是点
是点![]() 关于
关于![]() 轴,直线
轴,直线![]() :
:![]() 的二次对称点,则
的二次对称点,则![]() 的值为_______;
的值为_______;
③若点![]() 是点
是点![]() 关于
关于![]() 轴,直线
轴,直线![]() 的二次对称点,则直线
的二次对称点,则直线![]() 的表达式为__________;
的表达式为__________;
(2)如图2,![]() 的半径为1.若
的半径为1.若![]() 上存在点
上存在点![]() ,使得点
,使得点![]() 是点
是点![]() 关于
关于![]() 轴,直绩
轴,直绩![]() :
:![]() 的二次对称点,且点
的二次对称点,且点![]() 在射线
在射线![]() 上,
上,![]() 的取值范围是________;
的取值范围是________;
(3)![]() 是
是![]() 轴上的动点,
轴上的动点,![]() 的半径为2,若
的半径为2,若![]() 上存在点
上存在点![]() ,使得点
,使得点![]() 是点
是点![]() 关于
关于![]() 轴,直线
轴,直线![]() :
:![]() 的二次对称点,且点
的二次对称点,且点![]() 在
在![]() 轴上,求
轴上,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“长跑”是中考体育考试项目之一.某中学为了解九年级学生“长跑”的情况,随机抽取部分九年级学生,测试其长跑成绩(男子1000米,女子800米),按长跑的时间的长短依次分为A,B,C,D四个等级进行统计,并绘制成如下两幅不完整的统计图.请根据图中提供的信息,解答下列问题:
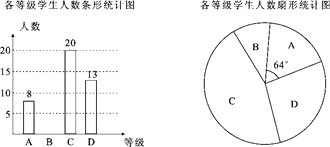
(1)在这次调查中共抽取了 名学生,扇形统计图中,D类所对应的扇形圆心角大小为 ;
(2)所抽取学生“长跑”测试成绩的中位数会落在 等级;
(3)若该校九年级共有900名学生,请你估计该校C等级的学生约在多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“新冠病毒”防控期间,某益康医疗器械公司分两次购进酒精消毒液与测温枪两种商品进行销售,两次购进同一商品的进价相同,具体情况如下表所示:
项目 | 购进数量(件) | 购进所需费用(元) | |
酒精消毒液 | 测温枪 | ||
第一次 | 30 | 40 | 8300 |
第二次 | 40 | 30 | 6400 |
(1)求酒精消毒液和测温枪两种商品每件的进价分别是多少元?
(2)公司决定酒精消毒液以每件20元出售,测温枪以每件240元出售.为满足市场需求,需购进这两种商品共1000件,且酒精消毒液的数量不少于测温枪数量的4倍,求该公司销售完上述1000件商品获得的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,依次连接第一个矩形各边的中点得到一个菱形,再依次连接菱形各边的中点得到第二个矩形,按照此方法继续下去.已知第一个矩形的两条邻边长分别为6和8,则第n个菱形的周长为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3,BC=4,点E为射线CB上一动点(不与点C重合),将△CDE沿DE所在直线折叠,点C落在点C′处,连接AC′,当△AC′D为直角三角形时,CE的长为_____.
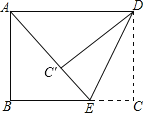
查看答案和解析>>
科目:初中数学 来源: 题型:
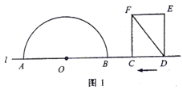
【题目】如图1,点![]() 和矩形
和矩形![]() 的边
的边![]() 都在直线
都在直线![]() 上,以点
上,以点![]() 为圆心,以24为半径作半圆,分别交直线
为圆心,以24为半径作半圆,分别交直线![]() 于
于![]() 两点.已知:
两点.已知: ![]() ,
,![]() ,矩形自右向左在直线
,矩形自右向左在直线![]() 上平移,当点
上平移,当点![]() 到达点
到达点![]() 时,矩形停止运动.在平移过程中,设矩形对角线
时,矩形停止运动.在平移过程中,设矩形对角线![]() 与半圆
与半圆![]() 的交点为
的交点为![]() (点
(点![]() 为半圆上远离点
为半圆上远离点![]() 的交点).
的交点).
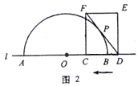
(1)如图2,若![]() 与半圆
与半圆![]() 相切,求
相切,求![]() 的值;
的值;
(2)如图3,当![]() 与半圆
与半圆![]() 有两个交点时,求线段
有两个交点时,求线段![]() 的取值范围;
的取值范围;
(3)若线段![]() 的长为20,直接写出此时
的长为20,直接写出此时![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
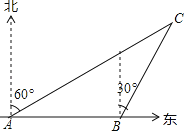
【题目】如图,一艘渔船以60海里每小时的速度向正东方向航行.在A处测得灯塔C在北偏东60°方向上;继续航行1小时到达B处,此时测得灯塔C在北偏东30°方向上.已知在灯塔C周围50海里范围内有暗礁,问这艘渔船继续向东航行有无触礁的危险?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com