Question

19．如图是一座抛物形拱桥，当水面的宽为12m时，拱顶离水面4m，当水面下降3m时，水面的宽为6$\sqrt{7}$m．

Answer 1

分析 根据题意可以建立相应的平面直角坐标系，从而可以求得抛物线的解析式，进而求得当水面下降3m时，水面的宽．

解答 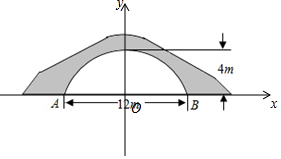解：以抛物线顶点为原点建立平面直角坐标系，如右图所示，
设抛物线的解析式为y=ax²，
∵点（6，-4）在函数图象上，
∴-4=a×6²，得a=$-\frac{1}{9}$，
∴y=$-\frac{1}{9}{x}^{2}$，
当y=-7时，
-7=$-\frac{1}{9}{x}^{2}$，
得${x}_{1}=-3\sqrt{7}$，${x}_{2}=3\sqrt{7}$，
∴当水面下降3m时，水面的宽为：$3\sqrt{7}-（-3\sqrt{7}）=6\sqrt{7}$m，
故答案为：6$\sqrt{7}$．

点评 本题考查二次函数的应用，解答此类问题的关键是建立合适的平面直角坐标系，求出相应的函数解析式，利用二次函数的性质解答．