
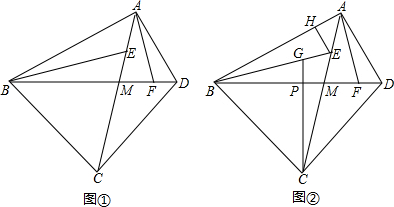
分析 (1)首先根据AC平分∠BAD,BE平分∠ABD,推得∠BEC=∠CBE,即可判断出CB=CE;然后根据CN⊥BE,推得∠BCN=∠ECN;最后推得CN∥AF,即可判断出∠BCE=2∠CAF.
(2)线段BD、CG、DF之间的数量关系为:BD-DF=$\frac{5}{4}$CG.首先作GI∥AB交AE于点I,作CN⊥BE于点N,延长BE交AF于点Q,CN与BP相交于点K,推得∠CDM=∠CBD,即可判断出BC=CD;然后根据相似三角形判定的方法,推得△BHE∽△BPG,即可判断出$\frac{BH}{BP}=\frac{BE}{BG}$=$\frac{15}{11}$,进而推得GI=$\frac{4}{15}$AB;最后根据相似三角形判定的方法,推得△GCI∽△EBA,即可判断出GI=$\frac{1}{3}$GC,进而判断出BD-DF=$\frac{5}{4}$CG即可.
解答 (1)证明:如图①,作CN⊥BE于点N,延长BE交AF于点Q,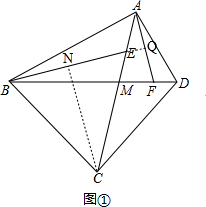 ,
,
∵AC平分∠BAD,
∴∠BAC=∠CAD,
∵BE平分∠ABD,
∴∠ABE=∠EBD,
∵∠BEC=∠ABE+∠BAE,∠CBE=∠EBD+∠DBC,∠DBC=∠CAD,
∴∠BEC=∠CBE,
∴CB=CE,
又∵CN⊥BE,
∴∠BCN=∠ECN,
∵点A关于直线BE的对称点F在BD上,
∴BQ⊥AF,
又∵CN⊥BE,
∴CN∥AF,
∴∠CAF=∠ECN=$\frac{1}{2}$∠BCE,
∴∠BCE=2∠CAF.
(2)解:线段BD、CG、DF之间的数量关系为:BD-DF=$\frac{5}{4}$CG.
如图②,作GI∥AB交AE于点I,作CN⊥BE于点N,延长BE交AF于点Q,CN与BP相交于点K,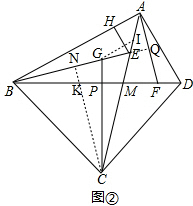 ,
,
∵∠CBM=∠DAM,∠CMB=∠DMA,
∴△CBM∽△DAM,
∴$\frac{AM}{MD}=\frac{BM}{MC}$,
又∵∠AMB=∠DMC,
∴△AMB∽△DMC,
∴∠BAM=∠CDM,
又∵∠BAM=∠DAM=∠CBD,
∴∠CDM=∠CBD,
∴BC=CD,
又∵BP⊥BD,
∴BP=PD,
∵∠ABE=∠EBD,∠BHE=∠BPG=90°,
∴△BHE∽△BPG,
∴$\frac{BH}{BP}=\frac{BE}{BG}$,
∵BH:BD=15:22,BD=2BP,
∴$\frac{BH}{BP}=\frac{BE}{BG}$=$\frac{15}{11}$,
∵GI∥AB,
∴∠EIG=∠EAB,
∴$\frac{GE}{BE}$=$\frac{GI}{AB}$=$\frac{4}{15}$,
∴GI=$\frac{4}{15}$AB,
∵A、F关于BE对称,
∴BA=BF,
∴∠BAF=∠BFA,
∵∠BNK=∠BPG=90°,∠BKN=∠CKP,
∴△BKN∽CKP,
∴∠KBN=∠KCP,
∴∠ABE=∠KBN=∠KCP,
∵∠BCE=4∠GCE,BC=CE,
∴∠GCI=∠KCP=∠ABE,
∴△GCI∽△EBA,
∴$\frac{GC}{GI}=\frac{BE}{AE}=3$,
∴GI=$\frac{1}{3}$GC,
又∵GI=$\frac{4}{15}$AB,
∴$\frac{1}{3}$GC=$\frac{4}{15}$AB,
∴AB=$\frac{5}{4}$CG,
∴BD-DF=BF=AB=$\frac{5}{4}$CG,
∴BD-DF=$\frac{5}{4}$CG.
点评 (1)此题主要考查了相似形综合题,考查了分析推理能力的应用,考查了数形结合思想的应用,要熟练掌握.
(2)此题还考查了三角形相似的判定和性质的应用,要熟练掌握,解答此题的关键是要明确:①三边法:三组对应边的比相等的两个三角形相似;②两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;③两角法:有两组角对应相等的两个三角形相似.


科目:初中数学 来源: 题型:解答题
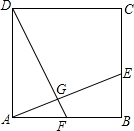 如图,已知点E、F分别为正方形ABCD的边BC、AB上的点,且AF=BE,AE与DF交于点G,试猜想AE与DF之间的大小关系和位置关系,并证明你的猜想.
如图,已知点E、F分别为正方形ABCD的边BC、AB上的点,且AF=BE,AE与DF交于点G,试猜想AE与DF之间的大小关系和位置关系,并证明你的猜想.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
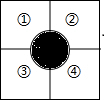 如图,一方形花坛分成编号为①、②、③、④四块,现有红、黄、蓝、紫四种颜色的花供选种.要求每块只种一种颜色的花,且相邻的两块种不同颜色的花,如果编号为①的已经种上红色花,那么其余三块不同的种法有( )种.
如图,一方形花坛分成编号为①、②、③、④四块,现有红、黄、蓝、紫四种颜色的花供选种.要求每块只种一种颜色的花,且相邻的两块种不同颜色的花,如果编号为①的已经种上红色花,那么其余三块不同的种法有( )种.| A. | 10 | B. | 20 | C. | 21 | D. | 15 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
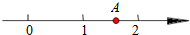 如图所示,在数轴上点A所表示的数x的范围是( )
如图所示,在数轴上点A所表示的数x的范围是( )| A. | $\frac{3}{2}$sin30°<x<sin60° | B. | cos30°<x<$\frac{3}{2}$cos45° | ||
| C. | $\frac{3}{2}$tan30°<x<tan45° | D. | $\frac{3}{2}$tan45°<x<tan60° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com