
【题目】如图(1),E是直线AB、CD内部一点,AB∥CD,连接EA、ED.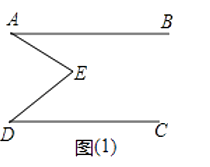
(1)探究:
①若∠A=30°,∠D=40°,则∠AED等于多少度?
②若∠A=20°,∠D=60°,则∠AED等于多少度?
③在图(1)中∠AED、∠EAB、∠EDC有什么数量关系,并证明你的结论.
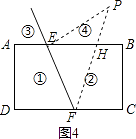
(2)拓展:如图(2),射线FE与矩形ABCD的边AB交于点E,与边CD交于点F,①②③④分别是被射线FE隔开的四个区域(不含边界,其中③④位于直线AB的上方),P是位于以上四个区域上点,猜想:∠PEB、∠PFC、∠EPF之间的关系.(不要求证明)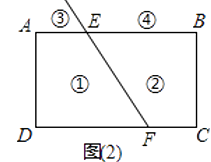
【答案】
(1)解:①如图①,过点E作EF∥AB,

∵AB∥CD,
∴AB∥CD∥EF,
∵∠A=30°,∠D=40°,
∴∠1=∠A=30°,∠2=∠D=40°,
∴∠AED=∠1+∠2=70°;
②过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∵∠A=20°,∠D=60°,
∴∠1=∠A=20°,∠2=∠D=60°,
∴∠AED=∠1+∠2=80°;
③猜想:∠AED=∠EAB+∠EDC.
理由:过点E作EF∥CD,
∵AB∥DC,
∴EF∥AB(平行于同一条直线的两直线平行),
∴∠1=∠EAB,∠2=∠EDC(两直线平行,内错角相等),
∴∠AED=∠1+∠2=∠EAB+∠EDC(等量代换).
(2)解:点P在区域①时,
如图1,在五边形EBCFP中,∠PEB+∠B+∠C+∠PFC+∠P=540°
∴∠EPF=540°﹣∠B﹣∠C﹣(∠PEB+∠PFC)=360°﹣(∠PEB+∠PFC);
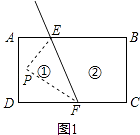
点P在区域②时,如图2,同(1)的方法得,∠EPF=∠PEB+∠PFC;
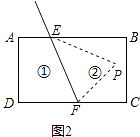
点P在区域③时,如图3,同(1)的方法得,∠EPF=∠PEB﹣∠PFC;
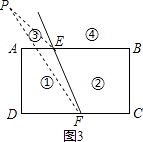
点P在区域④时,如图4,同(1)的方法得,∠EPF=∠PFC﹣∠PEB.
【解析】解阶梯式问题的基本策略是利用第1问的结论,特殊问题的方法可运用到一般问题中.


科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中的位置如图所示.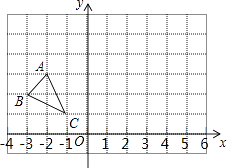
(1)在图中画出△ABC与关于y轴对称的图形△A1B1C1 , 并写出顶点A1、B1、C1的坐标;
(2)若将线段A1C1平移后得到线段A2C2 , 且A2(a,2),C2(﹣2,b),求a+b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.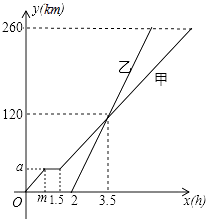
(1)求出图中m,a的值;
(2)求出甲车行驶路程y(km)与时间x(h)的函数解析式,并写出相应的x的取值范围;
(3)当乙车行驶多长时间时,两车恰好相距50km.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】农业部门引进一批新麦种,在播种前做了五次发芽试验,目的是想了解一粒这样的麦种发芽情况,实验统计数据如下:
实验的麦种数/粒 | 500 | 500 | 500 | 500 | 500 |
发芽的麦种数/粒 | 492 | 487 | 491 | 493 | 489 |
发芽率/% | 98.40 | 97.40 | 98.20 | 98.60 | 97.80 |
估计在与实验条件相同的情况下,种一粒这样的麦种发芽的概率约为
查看答案和解析>>
科目:初中数学 来源: 题型:
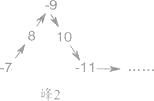
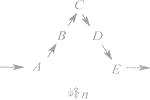
【题目】将一列数-1,2,-3,4,-5,6,……,如图所示有序排列.根据图中排列规律可知,“峰1” 中峰顶位置(C的位置)是4,那么,“峰206”中C的位置的有理数是 . 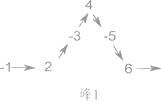
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com