
【题目】△ABC在平面直角坐标系中的位置如图所示.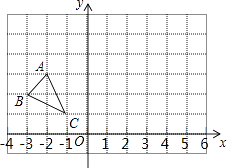
(1)在图中画出△ABC与关于y轴对称的图形△A1B1C1 , 并写出顶点A1、B1、C1的坐标;
(2)若将线段A1C1平移后得到线段A2C2 , 且A2(a,2),C2(﹣2,b),求a+b的值.
【答案】
(1)
解:如图所示:
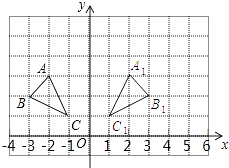
A1(2,3)、B1(3,2)、C1(1,1)
(2)
解:∵A1(2,3)、C1(1,1),A2(a,2),C2(﹣2,b).
∴将线段A1C1向下平移了1个单位,向左平移了3个单位.
∴a=﹣1,b=0.
∴a+b=﹣1+0=﹣1
【解析】(1)根据轴对称的性质确定出点A1、B1、C1的坐标,然后画出图形即可;(2)由点A1、C1的坐标,根据平移与坐标变化的规律可规定出a、b的值,从而可求得a+b的值.
【考点精析】解答此题的关键在于理解作轴对称图形的相关知识,掌握画对称轴图形的方法:①标出关键点②数方格,标出对称点③依次连线,以及对坐标与图形变化-平移的理解,了解新图形的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点;连接各组对应点的线段平行且相等.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
【题目】设a>b>0,c为常数,给出下列不等式①a﹣b>0;②ac>bc;③ ![]() <
< ![]() ;④b2>ab,其中正确的不等式有( )
;④b2>ab,其中正确的不等式有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△A′B′C′是由△ABC经过平移得到的,它们各顶点在平面直角坐标系中的坐标如下表所示:
△ABC | A(a,0) | B(3,0) | C(5,5) |
△A′B′C′ | A′(4,2) | B′(7,b) | C′(c,7) |
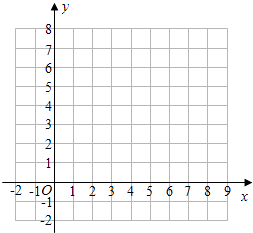
(1)观察表中各对应点坐标的变化,并填空:a= , b= , c=;
(2)在平面直角坐标系中画出△ABC及平移后的△A′B′C′;
(3)直接写出△A′B′C′的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点O(0,0),B(1,2).
(1)若点A在y轴的正半轴上,且三角形OAB的面积为2,求点A的坐标.
(2)若点A(3,0),BC∥OA,BC=OA,求点C的坐标.
(3)若点A(3,0),点D(3,﹣4),求四边形ODAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有三张反面朝上的扑克牌:红桃2、红桃3、黑桃x(1≤x≤13且x为奇数或偶数).把牌洗匀后第一次抽取一张,记好花色和数字后将牌放回,重新洗匀第二次再抽取一张.
(1)求两次抽得相同花色的概率;
(2)当甲选择x为奇数,乙选择x为偶数时,他们两次抽得的数字和是奇数的可能性大小一样吗?请说明理由.(提示:三张扑克牌可以分别简记为红2、红3、黑x)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,OA=7,OC=18,将点C先向上平移7个单位,再向左平移4个单位,得到点B,连接AB,BC.
(1)填空:点B的坐标为;
(2)如图2,BF平分∠ABC交x轴于点F,CD平分∠BCO交BF于点D,过点F作FH⊥BF交BC的延长线于点H,试判断DC与FH的位置关系,并说明理由;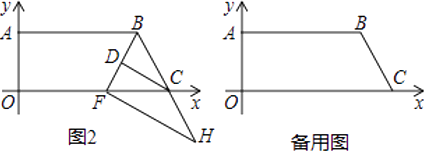
(3)若点P从点C出发以每秒2个单位长度的速度沿CO方向移动,同时点Q从点O出发以每秒1个单位长度的速度沿OA方向移动,设移动的时间为t秒(0<t<7),四边形OPBA与△OQB的面积分别记为S1,S2,是否存在一段时间,使S1<2S2?若存在,求出t的取值范围;若不存在,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),E是直线AB、CD内部一点,AB∥CD,连接EA、ED.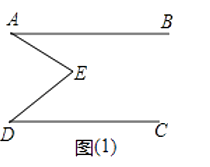
(1)探究:
①若∠A=30°,∠D=40°,则∠AED等于多少度?
②若∠A=20°,∠D=60°,则∠AED等于多少度?
③在图(1)中∠AED、∠EAB、∠EDC有什么数量关系,并证明你的结论.
(2)拓展:如图(2),射线FE与矩形ABCD的边AB交于点E,与边CD交于点F,①②③④分别是被射线FE隔开的四个区域(不含边界,其中③④位于直线AB的上方),P是位于以上四个区域上点,猜想:∠PEB、∠PFC、∠EPF之间的关系.(不要求证明)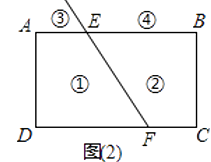
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com