
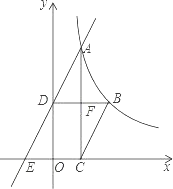
【题目】如图,已知函数y=![]() (x>0)的图象经过点A、B,点B的坐标为(2,2).过点A作AC⊥x轴,垂足为C,过点B作BD⊥y轴,垂足为D,AC与BD交于点F.一次函数y=ax+b的图象经过点A、D,与x轴的负半轴交于点E
(x>0)的图象经过点A、B,点B的坐标为(2,2).过点A作AC⊥x轴,垂足为C,过点B作BD⊥y轴,垂足为D,AC与BD交于点F.一次函数y=ax+b的图象经过点A、D,与x轴的负半轴交于点E
(1)若AC=![]() OD,求a、b的值;
OD,求a、b的值;
(2)若BC∥AE,求BC的长.
【答案】(10![]() ,b=2;(2)
,b=2;(2) ![]() .
.
【解析】
试题分析:(1)首先利用反比例函数图象上点的坐标性质得出k的值,再得出A、D点坐标,进而求出a,b的值;
(2)设A点的坐标为:(m,![]() ),则C点的坐标为:(m,0),得出tan∠ADF=
),则C点的坐标为:(m,0),得出tan∠ADF= ,tan∠AEC=
,tan∠AEC= ,进而求出m的值,即可得出答案.
,进而求出m的值,即可得出答案.
试题解析:(1)∵点B(2,2)在函数y=![]() (x>0)的图象上,
(x>0)的图象上,
∴k=4,则y=![]() ,
,
∵BD⊥y轴,∴D点的坐标为:(0,2),OD=2,
∵AC⊥x轴,AC=![]() OD,∴AC=3,即A点的纵坐标为:3,
OD,∴AC=3,即A点的纵坐标为:3,
∵点A在y=![]() 的图象上,∴A点的坐标为:(
的图象上,∴A点的坐标为:(![]() ,3),
,3),
∵一次函数y=ax+b的图象经过点A、D,
∴ ,
,
解得:![]() ,b=2;
,b=2;
(2)设A点的坐标为:(m,![]() ),则C点的坐标为:(m,0),
),则C点的坐标为:(m,0),
∵BD∥CE,且BC∥DE,
∴四边形BCED为平行四边形,
∴CE=BD=2,
∵BD∥CE,∴∠ADF=∠AEC,
∴在Rt△AFD中,tan∠ADF= ,
,
在Rt△ACE中,tan∠AEC= ,
,
∴![]() =
=![]() ,
,
解得:m=1,
∴C点的坐标为:(1,0),则BC=![]() .
.


科目:初中数学 来源: 题型:
【题目】某旅游团上午8时从旅馆出发,乘汽车到距离180千米的某著名旅游景点游玩,该汽车离旅馆的距离S(千米)与时间t (时)的关系可以用如图的折线表示.根据图象提供的有关信息,解答下列问题:
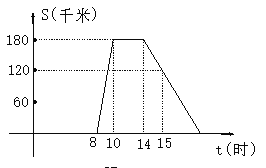
(1)求该团去景点时的平均速度是多少?
(2)该团在旅游景点游玩了多少小时?
(3)求出返程途中S(千米)与时间t (时)的函数关系式,并求出自变量t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面说法中正确的是 ( )
A. 两数之和为正,则两数均为正 B. 两数之和为负,则两数均为负
C. 两数之和为0,则这两数互为相反数 D. 两数之和一定大于每一个加数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用配方法解一元二次方程x2﹣8x﹣11=0时,下列变形正确的是( )
A. (x﹣4)2=5 B. (x+4)2=5 C. (x﹣4)2=27 D. (x+4)2=27
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小华和小丽最近测了自己的身高,小华量得自己约1.6m,小丽测得自己的身高约为1.60m,下列关于她俩身高的说法正确的是( )
(A)小华和小丽一样高;(B)小华比小丽高;(C)小华比小丽低;(D)无法确定谁高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:

(1)小明总共剪开了_______条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.
(3)小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是880cm,求这个长方体纸盒的体积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用两个全等的直角三角形拼下列图形:(1)平行四边形(不包含菱形、矩形、正方形);(2)矩形;(3)菱形;(4)正方形;(5)等腰三角形,一定可以拼成的图形是( )
A. (1)(2)(5) B. (2)(3)(5)
C. (1)(4)(5) D. (1)(2)(3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com