

 解:(1)如图1,BE=AF+EF.
解:(1)如图1,BE=AF+EF.
|


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
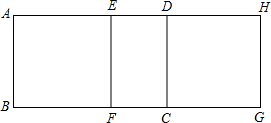 如图,长方形ABCD,AB=5cm,AD=8cm.若将该长方形沿AD方向平移一段距离,得到长方形EFGH,试问:
如图,长方形ABCD,AB=5cm,AD=8cm.若将该长方形沿AD方向平移一段距离,得到长方形EFGH,试问:查看答案和解析>>
科目:初中数学 来源: 题型:
 某校为绿化校园,在一块长为15米,宽为10米的长方形空地上建造一个长方形花圃,如图设计这个花圃的一边靠墙(墙长大于15米),并在不靠墙的三边留出一条宽相等的小路,设小路的宽为x米,花圃面积为为y平方米,求y关于x的函数解析式,并写出函数的定义域.
某校为绿化校园,在一块长为15米,宽为10米的长方形空地上建造一个长方形花圃,如图设计这个花圃的一边靠墙(墙长大于15米),并在不靠墙的三边留出一条宽相等的小路,设小路的宽为x米,花圃面积为为y平方米,求y关于x的函数解析式,并写出函数的定义域.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com