
【题目】如图,四边形![]() 是正方形,
是正方形,![]() 是等边三角形,
是等边三角形,![]() 为对角线
为对角线![]() (不含
(不含![]() 点)上任意一点,将
点)上任意一点,将![]() 绕点
绕点![]() 逆时针旋转60°得到
逆时针旋转60°得到![]() ,连接
,连接![]() 、
、![]() 、
、![]() .
.
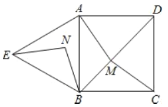
(1)求证![]() ;
;
(2)①当![]() 点在何处时,
点在何处时,![]() 的值最小;
的值最小;
②当![]() 点在何处时,
点在何处时,![]() 的值最小,并说明理由;
的值最小,并说明理由;
(3)当![]() 的最小值为
的最小值为![]() 时,求正方形的边长.
时,求正方形的边长.
【答案】(1)证明见解析;(2)①当M点落在BD的中点时,A、M、C三点共线,AM+CM的值最小.②如图,连接CE,当M点位于BD与CE的交点处时,AM+BM+CM的值最小.理由见解析;(3)![]() .
.
【解析】
(1)由题意得MB=NB,∠ABN=15°,所以∠EBN=45°,容易证出△AMB≌△ENB;
(2)①根据“两点之间线段最短”,可得,当M点落在BD的中点时,AM+CM的值最小;
②根据“两点之间线段最短”,当M点位于BD与CE的交点处时,AM+BM+CM的值最小,即等于EC的长(如图);
(3)作辅助线,过E点作EF⊥BC交CB的延长线于F,由题意求出∠EBF=30°,设正方形的边长为x,在Rt△EFC中,根据勾股定理求得正方形的边长为![]() .
.
(1)证明:∵△ABE是等边三角形,
∴BA=BE,∠ABE=60°.
∵∠MBN=60°,
∴∠MBN-∠ABN=∠ABE-∠ABN.
即∠MBA=∠NBE.
又∵MB=NB,
∴△AMB≌△ENB(SAS).
(2)解:①当M点落在BD的中点时,A、M、C三点共线,AM+CM的值最小.②如图,连接CE,当M点位于BD与CE的交点处时,
AM+BM+CM的值最小.
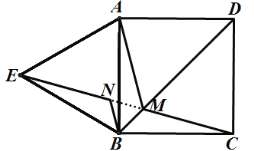
理由如下:连接MN,由(1)知,△AMB≌△ENB,
∴AM=EN,
∵∠MBN=60°,MB=NB,
∴△BMN是等边三角形.
∴BM=MN.
∴AM+BM+CM=EN+MN+CM.
根据“两点之间线段最短”可知,若E、N、M、C在同一条直线上时,EN+MN+CM取得最小值,最小值为EC.
在△ABM和△CBM中, ,
,
∴△ABM≌△CBM,
∴∠BAM=∠BCM,
∴∠BCM=∠BEN,
∵EB=CB,
∴若连接EC,则∠BEC=∠BCE,
∵∠BCM=∠BCE,∠BEN=∠BEC,
∴M、N可以同时在直线EC上.
∴当M点位于BD与CE的交点处时,AM+BM+CM的值最小,即等于EC的长.
(3)解:过E点作EF⊥BC交CB的延长线于F,
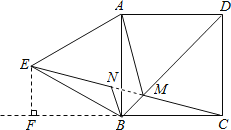
∴∠EBF=∠ABF-∠ABE=90°-60°=30°.
设正方形的边长为x,则BF=![]() x,EF=
x,EF=![]() .
.
在Rt△EFC中,
∵EF2+FC2=EC2,
∴(![]() )2+(
)2+(![]() x+x)2=(
x+x)2=(![]() +1)2.
+1)2.
解得x1=![]() ,x2=-
,x2=-![]() (舍去负值).
(舍去负值).
∴正方形的边长为![]() .
.


科目:初中数学 来源: 题型:
【题目】平面直角坐标系中有两点![]() 、
、![]() ,我们定义
,我们定义![]() 、
、![]() 两点间的“
两点间的“![]() 值”直角距离为
值”直角距离为![]() ,且满足
,且满足![]() ,其中
,其中![]() .小静和佳佳在解决问题:(求点
.小静和佳佳在解决问题:(求点![]() 与点
与点![]() 的“1值”直角距离
的“1值”直角距离![]() )时,采用了两种不同的方法:
)时,采用了两种不同的方法:
(方法一):![]() ;
;
(方法二):如图1,过点![]() 作
作![]() 轴于点
轴于点![]() ,过点
,过点![]() 作直线
作直线![]() 与
与![]() 轴交于点
轴交于点![]() ,则
,则![]()
请你参照以上两种方法,解决下列问题:
(1)已知点![]() ,点
,点![]() ,则
,则![]() 、
、![]() 两点间的“2值”直角距离
两点间的“2值”直角距离![]() .
.
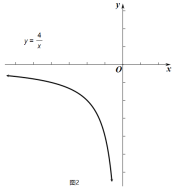
(2)函数![]() 的图像如图2所示,点
的图像如图2所示,点![]() 为其图像上一动点,满足
为其图像上一动点,满足![]() 两点间的“
两点间的“![]() 值”直角距离
值”直角距离![]() ,且符合条件的点
,且符合条件的点![]() 有且仅有一个,求出符合条件的“
有且仅有一个,求出符合条件的“![]() 值”和点
值”和点![]() 坐标.
坐标.
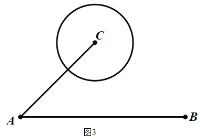
(3)城市的许多街道是相互垂直或平行的,因此,往往不能沿直线行走到达目的地,只能按直角拐弯的方式行走,因此,两地之间修建垂直和平行的街道常常转化为两点间的“![]() 值”直角距离,
值”直角距离,![]() 地位于
地位于![]() 地的正东方向上,
地的正东方向上,![]() 地在
地在![]() 点东北方向上且相距
点东北方向上且相距![]() ,以
,以![]() 为圆心修建了一个半径为
为圆心修建了一个半径为![]() 的圆形湿地公园,现在要在公园和
的圆形湿地公园,现在要在公园和![]() 地之间修建观光步道.步道只能东西或者南北走向,并且东西方向每千米成本是20万元,南北方向每千米的成本是10万元,问:修建这一规光步道至少要多少万元?
地之间修建观光步道.步道只能东西或者南北走向,并且东西方向每千米成本是20万元,南北方向每千米的成本是10万元,问:修建这一规光步道至少要多少万元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形![]() 是
是![]() 的内接四边形,
的内接四边形,![]() ,
,![]() ,垂足为
,垂足为![]() .
.
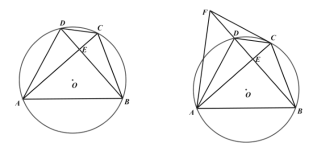
(1)如图1,求证:![]() ;
;
(2)如图2,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() ,连接
,连接![]() 、
、![]() ,求证:
,求证:![]() ;
;
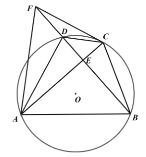
(3)如图3,在(2)的条件下,若![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人加工同一种零件,甲每天加工的数量是乙每天加工数量的 1.5 倍,两人各加工 600 个这种零件,甲比乙少用 5 天.
(1)求甲、乙两人每天各加工多少个这种零件?
(2)已知甲、乙两人加工这种零件每天的加工费分别是 150 元和 120 元,现有 3000 个这种零件的加工任务,甲单独加工一段时间后另有安排,剩余任务由乙单独完成.如果总加工费不超过 7800 元,那么甲至少加工了多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线D′处.若AB=3,AD=4,则ED的长为

A.![]() B.3 C.1 D.
B.3 C.1 D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应市政府关于“垃圾不落地,市区更美丽”的主题宣传活动,某校随机调查了部分学生对垃圾分类知识的了解情况,对该校部分学生进行了问卷调查,并将调查结果分为![]() 四类(其中
四类(其中![]() 类表示“非常了解”,
类表示“非常了解”,![]() 类表示“比较了解”,
类表示“比较了解”,![]() 类表示“基本了解”,
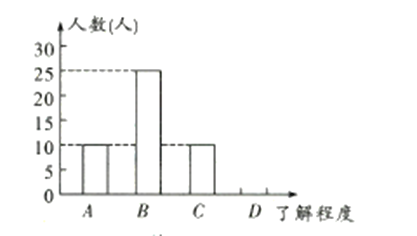
类表示“基本了解”,![]() 类表示“不太了解”).根据调查结果得到如下不完整的统计表和统计图.请解答下列问题:
类表示“不太了解”).根据调查结果得到如下不完整的统计表和统计图.请解答下列问题:
了解程度 | 人数(人) | 所占百分比 |
|
|
|
|
|
|
|
|
|
|
|
|
![]() ,
,![]() .
.
![]() 补全条形统计图;
补全条形统计图;
![]() 若该校共有学生
若该校共有学生![]() 人,估计该校对垃圾分类知识“非常了解”的有多少人?
人,估计该校对垃圾分类知识“非常了解”的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC中,∠ACB=90°,D在斜边AB上,DE⊥AC,DF⊥BC,垂足分别为E,F.
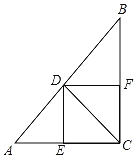
(1)当∠ACD=∠BCD时,求证:四边形DECF是正方形;
(2)当∠BCD=∠A时,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为2的正方形![]() 中,
中,![]() 为
为![]() 的中点,
的中点,![]() 为边
为边![]() 上一动点,设
上一动点,设![]() ,线段
,线段![]() 的垂直平分线分别交边
的垂直平分线分别交边![]() 、
、![]() 于点
于点![]() 、
、![]() ,过
,过![]() 作
作![]() 于点
于点![]() ,过
,过![]() 作
作![]() 于点
于点![]() .
.
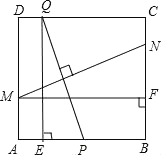
(1)当![]() 时,求证:
时,求证:![]() ;
;
(2)顺次连接![]() 、
、![]() 、
、![]() 、
、![]() ,设四边形
,设四边形![]() 的面积为
的面积为![]() ,求出
,求出![]() 与自变量
与自变量![]() 之间的函数关系式,并求
之间的函数关系式,并求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com