
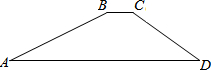
 如图,一水库大坝的横断面为梯形ABCD,坝顶BC宽6米,坝高20米,斜坡AB的坡度i=1:2.5,斜坡CD的坡角为30度,则坝底AD的长度为( )
如图,一水库大坝的横断面为梯形ABCD,坝顶BC宽6米,坝高20米,斜坡AB的坡度i=1:2.5,斜坡CD的坡角为30度,则坝底AD的长度为( )| A. | 56米 | B. | 66米 | C. | (56+20$\sqrt{3}$)米 | D. | (50$\sqrt{2}$+20$\sqrt{3}$)米 |
分析 过梯形上底的两个顶点向下底引垂线,得到两个直角三角形和一个矩形,利用相应的性质求解即可.
解答 解:作BE⊥AD,CF⊥AD,垂足分别为点E,F,则四边形BCFE是矩形,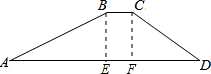
由题意得,BC=EF=6米,BE=CF=20米,斜坡AB的坡度i为1:2.5,
在Rt△ABE中,
∵$\frac{BE}{AE}$=$\frac{1}{2.5}$,
∴AE=50米,
在Rt△CFD中,
∵∠D=30°,
∴DF=CFcot∠D=20$\sqrt{3}$米,
∴AD=AE+EF+FD=50+6+20$\sqrt{3}$=(56+20$\sqrt{3}$)米.
故选C.
点评 本题考查了坡度及坡角的知识,解答本题的关键是构造直角三角形和矩形,注意理解坡度与坡角的定义.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:选择题
 如图,⊙O中,AD、BC是圆O的弦,OA⊥BC,∠AOB=50°,CE⊥AD,则∠DCE的度数是( )
如图,⊙O中,AD、BC是圆O的弦,OA⊥BC,∠AOB=50°,CE⊥AD,则∠DCE的度数是( )| A. | 25° | B. | 65° | C. | 45° | D. | 55° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
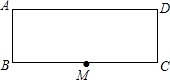 如图,在矩形ABCD中,AB=5,BC=24,M是BC的中点,若点P为线段AD上的一点,连接AM、PM,△PAM是以AP为腰的等腰三角形,则AP的长为13或$\frac{169}{24}$.
如图,在矩形ABCD中,AB=5,BC=24,M是BC的中点,若点P为线段AD上的一点,连接AM、PM,△PAM是以AP为腰的等腰三角形,则AP的长为13或$\frac{169}{24}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知∠AOB=60°,点P在边OA上,OP=8,点M,N在边OB上,PM=PN,若MN=2,则ON=( )
如图,已知∠AOB=60°,点P在边OA上,OP=8,点M,N在边OB上,PM=PN,若MN=2,则ON=( )| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
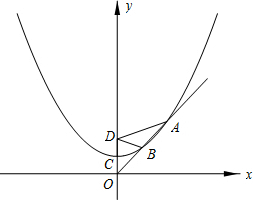 已知抛物线的顶点是C(0,m)(m>0,m为常数),并经过点(2m,2m),点D(0,2m)为一定点.
已知抛物线的顶点是C(0,m)(m>0,m为常数),并经过点(2m,2m),点D(0,2m)为一定点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com