
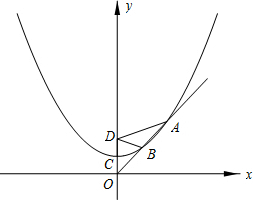
 已知抛物线的顶点是C(0,m)(m>0,m为常数),并经过点(2m,2m),点D(0,2m)为一定点.
已知抛物线的顶点是C(0,m)(m>0,m为常数),并经过点(2m,2m),点D(0,2m)为一定点.分析 (1)由条件可设出抛物线的解析式,再把(2m,2m)坐标代入可求得抛物线解析式;
(2)设P(x,y),分别过P作PH⊥x轴,PG⊥y轴,结合条件可分别用m表示出PD和PH,可得到PD=PH;
(3)过B作BE⊥xAF⊥y轴,结合(2)的结论可得到B、C分别为OA、OD的中点,可求得B点坐标,从而可表示出△ABD和△OBD的面积,整理可求得m的值.
解答 解:(1)根据题意可设抛物线的解析式为y=kx2+m,
∵点(2m,2m)在抛物线上,
∴4m2k+m=2m,解得k=$\frac{1}{4m}$,
∴抛物线的解析式为y=$\frac{1}{4m}$x2+m;
(2)PD=PH.理由如下:
设抛物线上一点P(x,y),过P作PH⊥x轴,PG⊥y轴,垂足分别为H、G,连接PD,如图1,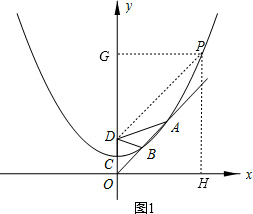
在Rt△GDP中,由勾股定理得:PD2=DG2+PG2=(y-2m)2+x2=y2-4my+4m2+x2,
又P点在抛物线上,
∴y=$\frac{1}{4m}$x2+m,
∴x2=4m(y-m)=4my-4m2,
∴PD2=y2-4my+4m2+4my-4m2=y2=PH2,
∴PD=PH;
(3)过B作BE⊥x轴,过A作AF⊥y轴,垂足分别为E、F,连接BC,过B作BR⊥y轴于点R,如图2,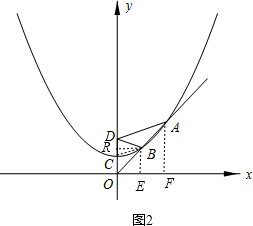
由(2)的结论:BE=BD,AF=DA,
∵DA=2DB,
∴AF=2BE,
∴AO=2BO,
∴B是OA中点,且C是OD的中点,
∴BC=$\frac{1}{2}$DA=$\frac{1}{2}$AF=BE=BD,
∵BR⊥CD,
∴CR=DR,OR=m+$\frac{1}{2}$m=$\frac{3}{2}$m,
∴B点纵坐标是$\frac{3}{2}$m,又点B在抛物线上,
∴$\frac{3}{2}$m=$\frac{1}{4m}$x2+m,整理可得x2=2m2,
∵x>0,
∴x=$\sqrt{2}$m,
∴B点坐标为($\sqrt{2}$m,$\frac{3}{2}$m),
又AO=2PB.
∴S△ABD=S△OBD=4$\sqrt{2}$,
∴$\frac{1}{2}$×2m×$\sqrt{2}$m=4$\sqrt{2}$,
∴m2=4,
∵m>0,
∴m=2.
点评 本题主要考查二次函数的综合应用,涉及知识点有待定系数法、勾股定理、三角形面积等知识点.在(1)中注意关于y轴对称的抛物线的解析式的形式,在(2)中用m分别表示出PD和PH是解题的关键,在(3)中用m表示出B点的坐标是解题的关键.本题考查知识均为基础知识,难度适中.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:初中数学 来源: 题型:选择题
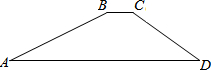 如图,一水库大坝的横断面为梯形ABCD,坝顶BC宽6米,坝高20米,斜坡AB的坡度i=1:2.5,斜坡CD的坡角为30度,则坝底AD的长度为( )
如图,一水库大坝的横断面为梯形ABCD,坝顶BC宽6米,坝高20米,斜坡AB的坡度i=1:2.5,斜坡CD的坡角为30度,则坝底AD的长度为( )| A. | 56米 | B. | 66米 | C. | (56+20$\sqrt{3}$)米 | D. | (50$\sqrt{2}$+20$\sqrt{3}$)米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
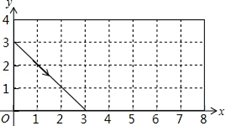 如图,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点P第2015次碰到矩形的边时,点P的坐标为( )
如图,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点P第2015次碰到矩形的边时,点P的坐标为( )| A. | (3,0) | B. | (7,4) | C. | (8,1) | D. | (1,4) |
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省南通市七年级3月月考数学试卷(解析版) 题型:单选题
如图,根据下列条件不可以判定a∥b的是( )
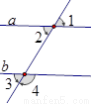
A. ∠2=∠3 B. ∠1= ∠3 C. ∠1= ∠4 D. ∠1 +∠4 =180°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com