
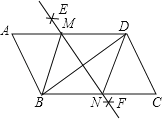
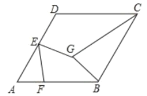
【题目】如图,BD是ABCD的对角线,按以下步骤作图:①分别以点B和点D为圆心,大于![]() BD的长为半径作弧,两弧相交于E,F两点;②作直线EF,分别交AD,BC于点M,N,连接BM,DN.若BD=8,MN=6,则ABCD的边BC上的高为___.
BD的长为半径作弧,两弧相交于E,F两点;②作直线EF,分别交AD,BC于点M,N,连接BM,DN.若BD=8,MN=6,则ABCD的边BC上的高为___.
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:
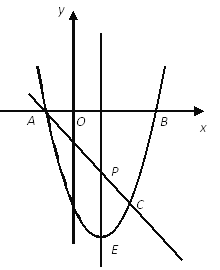
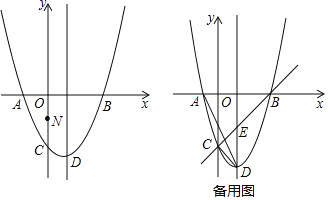
【题目】如图,抛物线![]() 与x轴交A、B两点(A点在B点左侧),直线
与x轴交A、B两点(A点在B点左侧),直线![]() 与抛物线交于A、C两点,其中C点的横坐标为2.
与抛物线交于A、C两点,其中C点的横坐标为2.
(1)求A、B两点的坐标及直线AC的函数表达式;
(2)P是线段AC上的一个动点,过P点作y轴的平行线交抛物线于E点,求线段PE长度的最大值;
(3)点G是抛物线上的动点,在x轴上是否存在点F,使A、C、F、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+2(m+1)x+m21=0.
(1)若方程有两个不相等的实数根,求实数m的取值范围;
(2)若方程两实数根分别为x1,x2,且满足x1+x2+x1x2=5,求实数m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中有4个大小、质地完全相同的乒乓球,球面上分别标有数-1,2,-3,4.
(1)摇匀后任意摸出1个球,则摸出的乒乓球球面上的数是负数的概率为________.
(2)摇匀后先从中任意摸出1个球(不放回),再从余下的3个球中任意摸出1个球,用列表或画树状图的方法求两次摸出的乒乓球球面上的数之和是正数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
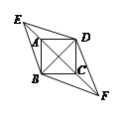
【题目】如图,正方形ABCD的边长为3![]() ,对角线AC、BD相交于点O,将AC向两个方向延长,分别至点E和点F,且AE=CF=3,则四边形BEDF的周长为( )
,对角线AC、BD相交于点O,将AC向两个方向延长,分别至点E和点F,且AE=CF=3,则四边形BEDF的周长为( )
A. 20B. 24C. 12![]() D. 12
D. 12![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD为正方形,点E为线段AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
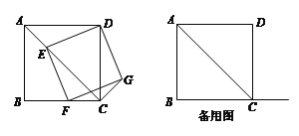
(1)如图,求证:矩形DEFG是正方形;
(2)若AB=2![]() ,CE=2,求CG的长;
,CE=2,求CG的长;
(3)当直线DE与正方形ABCD的某条边所夹锐角是40°时,直接写出∠EFC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是抛物线的顶点.
是抛物线的顶点.
(1)求抛物线的解析式.
(2)点![]() 是
是![]() 轴负半轴上的一点,且
轴负半轴上的一点,且![]() ,点
,点![]() 在对称轴右侧的抛物线上运动,连接
在对称轴右侧的抛物线上运动,连接![]() ,
,![]() 与抛物线的对称轴交于点
与抛物线的对称轴交于点![]() ,连接
,连接![]() ,当
,当![]() 平分
平分![]() 时,求点
时,求点![]() 的坐标.
的坐标.
(3)直线![]() 交对称轴于点
交对称轴于点![]() ,
,![]() 是坐标平面内一点,请直接写出
是坐标平面内一点,请直接写出![]() 与
与![]() 全等时点
全等时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边长为4,∠A=60°,E是边AD的中点,F是边BC上的一个动点,EG=EF,且∠GEF=60°,则GB+GC的最小值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形OABC的顶点A(-8,0)、C(0,6),点D是BC边上的中点,抛物线y=ax2+bx经过A、D两点,如图所示.
(1)求点D关于y轴的对称点D′的坐标及a、b的值;
(2)在y轴上取一点P,使PA+PD长度最短,求点P的坐标;
(3)将抛物线y=ax2+bx向下平移,记平移后点A的对应点为A1,点D的对应点为D1,当抛物线平移到某个位置时,恰好使得点O是y轴上到A1、D1两点距离之和OA1+OD1最短的一点,求此抛物线的解析式.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com