
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是抛物线的顶点.
是抛物线的顶点.
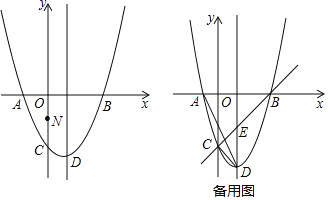
(1)求抛物线的解析式.
(2)点![]() 是
是![]() 轴负半轴上的一点,且
轴负半轴上的一点,且![]() ,点
,点![]() 在对称轴右侧的抛物线上运动,连接
在对称轴右侧的抛物线上运动,连接![]() ,
,![]() 与抛物线的对称轴交于点
与抛物线的对称轴交于点![]() ,连接
,连接![]() ,当
,当![]() 平分
平分![]() 时,求点
时,求点![]() 的坐标.
的坐标.
(3)直线![]() 交对称轴于点
交对称轴于点![]() ,
,![]() 是坐标平面内一点,请直接写出
是坐标平面内一点,请直接写出![]() 与
与![]() 全等时点
全等时点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)点
;(2)点![]() 的坐标为:
的坐标为:![]() ,
,![]() ;(3)若
;(3)若![]() 与
与![]() 全等,
全等,![]() 点有四个,坐标为
点有四个,坐标为![]() ,
,![]() ,
,![]() ,
,![]() .
.
【解析】
(1)用待定系数法,直接将![]() 代入解析式即可求解.
代入解析式即可求解.
(2)由![]() 平分
平分![]() ,
,![]() 平行
平行![]() 即可求出
即可求出![]() ,继而得出
,继而得出![]() 点坐标,由直线
点坐标,由直线![]() 解析式即可求出与抛物线交点坐标
解析式即可求出与抛物线交点坐标![]() 即可.
即可.
(3)由![]() 三点的坐标可得
三点的坐标可得![]() 三边长,由
三边长,由![]() 坐标可得
坐标可得![]() 和
和![]() 中
中![]() ,则另两组边对应相等即可,设
,则另两组边对应相等即可,设![]() 点坐标为
点坐标为![]() ;利用两点间距离公式即列方程求解.
;利用两点间距离公式即列方程求解.
(1)![]() 抛物线
抛物线![]() 经过
经过![]() ,
,![]() 两点,
两点,
![]()
![]() ,
,
解得:![]() ,
,
![]() 抛物线的解析式为:
抛物线的解析式为:![]() .
.
(2)如图1,设对称轴与![]() 轴交于点
轴交于点![]() ,
,

![]() 平分
平分![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
在![]() 中,
中,![]() ,
,![]() .
.
![]()
![]() ,
,
![]() ;
;![]() .
.
①当![]() 时,直线
时,直线![]() 解析式为:
解析式为:![]() ,
,
依题意得:![]() .
.
解得:![]() ,
,![]() ,
,
![]() 点
点![]() 在对称轴右侧的抛物线上运动,
在对称轴右侧的抛物线上运动,
![]() 点纵坐标
点纵坐标![]() .
.
![]()
![]() ,
,
②当![]() 时,直线
时,直线![]() 解析式为:
解析式为:![]() ,
,
同理可求:![]() ,
,
综上所述:点![]() 的坐标为:
的坐标为:![]() ,
,![]() ,
,
(3)由题意可知:![]() ,
,![]() ,
,![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 直线
直线![]() 经过
经过![]() ,
,![]() ,
,
![]() 直线
直线![]() 解析式为
解析式为![]() ,
,
![]() 抛物线对称轴为
抛物线对称轴为![]() ,而直线
,而直线![]() 交对称轴于点
交对称轴于点![]() ,
,
![]() 坐标为
坐标为![]() ;
;
![]() ,
,
设![]() 点坐标为
点坐标为![]() ,
,
则![]() ,
,
则![]() ,
,
![]() ,若
,若![]() 与
与![]() 全等,有两种情况,
全等,有两种情况,
Ⅰ.![]() ,
,![]() ,即
,即![]() .
.
![]()
 ,
,
解得: ,
, ,
,
即![]() 点坐标为
点坐标为![]() ,
,![]() .
.
Ⅱ.![]() ,
,![]() ,即
,即![]() .
.
![]()
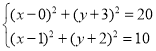 ,
,
解得: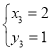 ,
, ,
,
即![]() 点坐标为
点坐标为![]() ,
,![]() .
.
故若![]() 与
与![]() 全等,
全等,![]() 点有四个,坐标为
点有四个,坐标为![]() ,
,![]() ,
,![]() ,
,![]() .
.


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2﹣2x﹣3与x轴交于点A(﹣1,0),点B(3,0),与y轴交于点C,点D是该抛物线的顶点,连接AD,BD.

(1)直接写出点C、D的坐标;
(2)求△ABD的面积;
(3)点P是抛物线上的一动点,若△ABP的面积是△ABD面积的![]() ,求点P的坐标.
,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知BC是⊙O的直径,A是⊙O上一点,AD⊥BC,垂足为D,![]() =
=![]() ,BE交AD于点F.
,BE交AD于点F.
(1)∠ACB与∠BAD相等吗?为什么?
(2)判断△FAB的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是ABCD的对角线,按以下步骤作图:①分别以点B和点D为圆心,大于![]() BD的长为半径作弧,两弧相交于E,F两点;②作直线EF,分别交AD,BC于点M,N,连接BM,DN.若BD=8,MN=6,则ABCD的边BC上的高为___.
BD的长为半径作弧,两弧相交于E,F两点;②作直线EF,分别交AD,BC于点M,N,连接BM,DN.若BD=8,MN=6,则ABCD的边BC上的高为___.
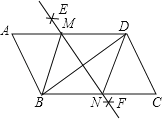
查看答案和解析>>
科目:初中数学 来源: 题型:
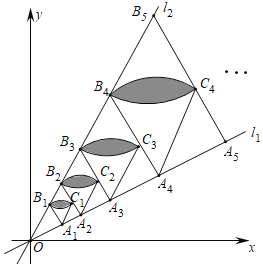
【题目】如图,直线l1的解析式是![]() ,直线l2的解析式是
,直线l2的解析式是![]() ,点A1在l1上,A1的横坐标为
,点A1在l1上,A1的横坐标为![]() ,作
,作![]() 交l2于点B1,点B2在l2上,以B1A1,B1B2为邻边在直线l1,l2间作菱形A1B1B2C1,分别以点A1,B2为圆心,以A1B1为半径画弧得扇形B1A1C1和扇形B1B2C1,记扇形B1A1C1与扇形B1B2C1重叠部分的面积为S1;延长B2C1交l1于点A2,点B3在l2上,以B2A2,B2B3为邻边在l1,l2间作菱形A2B2B3C2,分别以点A2,B3为圆心,以A2B2为半径画弧得扇形B2A2C2和扇形B2B3C2,记扇形B2A2C2与扇形B2B3C2重叠部分的面积为S2……按照此规律继续作下去,则
交l2于点B1,点B2在l2上,以B1A1,B1B2为邻边在直线l1,l2间作菱形A1B1B2C1,分别以点A1,B2为圆心,以A1B1为半径画弧得扇形B1A1C1和扇形B1B2C1,记扇形B1A1C1与扇形B1B2C1重叠部分的面积为S1;延长B2C1交l1于点A2,点B3在l2上,以B2A2,B2B3为邻边在l1,l2间作菱形A2B2B3C2,分别以点A2,B3为圆心,以A2B2为半径画弧得扇形B2A2C2和扇形B2B3C2,记扇形B2A2C2与扇形B2B3C2重叠部分的面积为S2……按照此规律继续作下去,则![]() ________.(用含有正整数n的式子表示)
________.(用含有正整数n的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠ACB=90°,CE是中线,△ACD与△ACE关于直线AC对称.

(1)求证:四边形ADCE是菱形;
(2)求证:BC=ED.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果店张阿姨以每斤4元的价格购进某种水果若干斤,然后以每斤6元的价格出售,每天可售出150斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出30斤,为保证每天至少售出360斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利450元,张阿姨需将每斤的售价降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】人民商场销售某种商品,统计发现:每件盈利![]() 元时,平均每天可销售
元时,平均每天可销售![]() 件.经调查发现,该商品每降价
件.经调查发现,该商品每降价![]() 元,商场平均每天可多售出
元,商场平均每天可多售出![]() 件.
件.
![]() 假如现在库存量太大,部门经理想尽快减少库存,又想销售该商品日盈利达到
假如现在库存量太大,部门经理想尽快减少库存,又想销售该商品日盈利达到![]() 元,请你帮忙思考,该降价多少?
元,请你帮忙思考,该降价多少?
![]() 假如部门经理想销售该商品的日盈利达到最大,请你帮忙思考,又该如何降价?
假如部门经理想销售该商品的日盈利达到最大,请你帮忙思考,又该如何降价?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读:我们约定,在平面直角坐标系中,经过某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线,叫该点的“特征线”.例如,点M(1,3)的特征线有:x=1,y=3,y=x+2,y=x+4.如图,在平面直角坐标系中有正方形OABC,点B在第一象限,A、C分别在x轴和y轴上,抛物线![]() 经过B.C两点,顶点D在正方形内部.
经过B.C两点,顶点D在正方形内部.
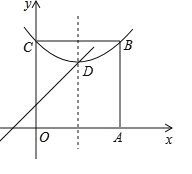
(1)写出点M(2,3)任意两条特征线___________________
(2)若点D有一条特征线是y=x+1,求此抛物线的解析式________________________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com