
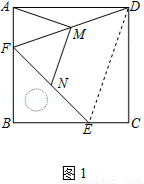
把一个含45°角的直角三角板BEF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点B重合,联结DF,点M,N分别为DF,EF的中点,联结MA,MN.
(1)如图1,点E,F分别在正方形的边CB,AB上,请判断MA,MN的数量关系和位置关系,直接
写出结论;
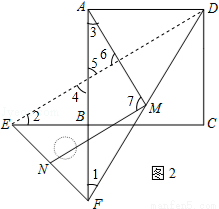
(2)如图2,点E,F分别在正方形的边CB,AB的延长线上,其他条件不变,那么你在(1)中得到的两个结论还成立吗?若成立,请加以证明;若不成立,请说明理由.


图1 图2
(1)MA=MN,MA⊥MN;(2)成立,理由详见解析
【解析】
试题分析:(1)连接DE,先根据直角三角形的性质得出AM= DF,再根据△BEF是等腰直角三角形得出AF=CE,由SAS定理得出△ADF≌△CDE,故DE=DF.再根据点M,N分别为DF,EF的中点,得出MN是△EFD的中位线,故MN=
DF,再根据△BEF是等腰直角三角形得出AF=CE,由SAS定理得出△ADF≌△CDE,故DE=DF.再根据点M,N分别为DF,EF的中点,得出MN是△EFD的中位线,故MN= DE,MN∥DE,再根据平行线的性质及全等三角形的性质即可得出结论;
DE,MN∥DE,再根据平行线的性质及全等三角形的性质即可得出结论;
(2)连接DE,由直角三角形的性质得出MA=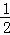 DF=MD=MF,故∠1=∠3.再由点N是EF的中点,得出MN是△DEF的中位线,所以MN=
DF=MD=MF,故∠1=∠3.再由点N是EF的中点,得出MN是△DEF的中位线,所以MN=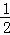 DE,MN∥DE.根据△BEF是等腰直角三角形可知BF=BF,∠EBF=90°.根据SAS定理得出△ADF≌△CDE,故DF=DE,∠1=∠2,MA=MN,∠2=∠3.再根据∠2+∠4=∠ABC=90°,∠4=∠5得出∠3+∠5=90°,由三角形内角和定理可知∠6=180°﹣(∠3+∠5)=90°,故可得出结论.
DE,MN∥DE.根据△BEF是等腰直角三角形可知BF=BF,∠EBF=90°.根据SAS定理得出△ADF≌△CDE,故DF=DE,∠1=∠2,MA=MN,∠2=∠3.再根据∠2+∠4=∠ABC=90°,∠4=∠5得出∠3+∠5=90°,由三角形内角和定理可知∠6=180°﹣(∠3+∠5)=90°,故可得出结论.
试题解析:(1)【解析】
连接DE,
∵四边形ABCD是正方形,
∴AD=CD=AB=BC,∠DAB=∠DCE=90°,
∵点M是DF的中点,
∴AM=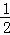 DF.
DF.
∵△BEF是等腰直角三角形,
∴AF=CE,
在△ADF与△CDE中,
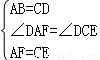 ,
,
∴△ADF≌△CDE(SAS),
∴DE=DF.
∵点M,N分别为DF,EF的中点,
∴MN是△EFD的中位线,
∴MN=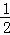 DE,
DE,
∴AM=MN;
∵MN是△EFD的中位线,
∴MN∥DE,
∴∠FMN=∠FDE.
∵AM=MD,
∴∠MAD=∠ADM,
∵∠AMF是△ADM的中位线,
∴∠AMF=2∠ADM.
∵△ADF≌△CDE,
∴∠ADM=∠DEC,
∴∠ADM+∠DEC+∠FDE=∠FMN+∠AMF=90°,
∴MA⊥MN.
∴MA=MN,MA⊥MN.
(2)成立.
理由:连接DE.
∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠ABC=∠BCD=∠CDA=∠DAB=90°.
在Rt△ADF中,
∵点M是DF的中点,
∴MA=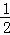 DF=MD=MF,
DF=MD=MF,
∴∠1=∠3.
∵点N是EF的中点,
∴MN是△DEF的中位线,
∴MN=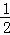 DE,MN∥DE.
DE,MN∥DE.
∵△BEF是等腰直角三角形,
∴BF=BF,∠EBF=90°.
∵点E、F分别在正方形CB、AB的延长线上,
∴AB+BF=CB+BE,即AF=CE.
在△ADF与△CDE中,
∵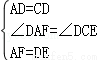
∴△ADF≌△CDE,
∴DF=DE,∠1=∠2,
∴MA=MN,∠2=∠3.
∵∠2+∠4=∠ABC=90°,∠4=∠5,
∴∠3+∠5=90°,
∴∠6=180°﹣(∠3+∠5)=90°,
∴∠7=∠6=90°,MA⊥MN.
考点:四边形综合题


科目:初中数学 来源:2015届北京市八年级下学期期中数学试卷(解析版) 题型:解答题
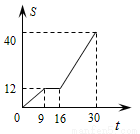
是某汽车行驶的路程S(km)与时间t(min)的函数关系图.观察图中所提供的信息,解答下列问题:
(1)汽车在前9分钟内的平均速度是多少?
(2)汽车在中途停了多长时间?
(3)当16≤t≤30时,求S与t的函数关系式.
查看答案和解析>>
科目:初中数学 来源:2015届北京市房山区八年级下学期期末考试数学试卷(解析版) 题型:选择题
在一个不透明的盒子中放有2个黄色乒乓球和4个白色乒乓球,所有乒乓球除颜色外完全相同,从中随机摸出1个乒乓球,摸出白色乒乓球的概率为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2015届北京市大兴区八年级下学期期末考试数学试卷(解析版) 题型:填空题
如果关于x的一元二次方程x2﹣6x+c=0(c是常数)没有实根,那么c的取值范围是 .
查看答案和解析>>
科目:初中数学 来源:2015届北京市大兴区八年级下学期期末考试数学试卷(解析版) 题型:选择题
下列命题中,真命题是( )
A.有两边相等的平行四边形是菱形
B.有一个角是直角的四边形是直角梯形
C.四个角相等的菱形是正方形
D.两条对角线相等的四边形是矩形
查看答案和解析>>
科目:初中数学 来源:2015届北京市丰台区八年级下学期期末考试数学试卷(解析版) 题型:解答题
已知关于 的一元二次方程
的一元二次方程 有两个不相等的实数根.
有两个不相等的实数根.
(1)求 的取值范围;
的取值范围;
(2)若 为正整数,且该方程的根都是整数,求
为正整数,且该方程的根都是整数,求 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:2015届云南省八年级上学期期末考试数学试卷(解析版) 题型:解答题
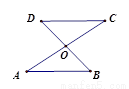
如图,AC交BD于点O,请你从三项中选出两个作为条件,另一个作为结论,写出一个真命题,并加以证明.
①OA=OC ②OB=OD ③AB∥CD
查看答案和解析>>
科目:初中数学 来源:2014年江西省吉安市吉州区九年级下学期第一次中考模拟数学试卷(解析版) 题型:选择题
吉州区“人文社区,温馨家园”建设被推荐参加2013年中国社区治理十大创新成果。2014年进行了网络投票,截止到3月7日共收到投票3680000张,这个数用科学计数法表示为( )
A.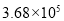 B.
B.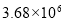 C.
C.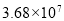 D.
D.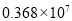
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com