
分析 (1)根据有理数的混合运算的运算方法,求出算式的值是多少即可.
(2)应用乘法分配律,求出算式的值是多少即可.
解答 解:(1)(-1)4+$\frac{28}{5}$÷(-2)×(-$\frac{5}{14}$)
=1+(-$\frac{14}{5}$)×(-$\frac{5}{14}$)
=1+1
=2
(2)(-$\frac{3}{4}$+1$\frac{5}{6}$-$\frac{7}{8}$)×(-24)
=(-$\frac{3}{4}$)×(-24)+1$\frac{5}{6}$×(-24)-$\frac{7}{8}$×(-24)
=18-44+21
=-5
点评 此题主要考查了有理数的混合运算,要熟练掌握,注意明确有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
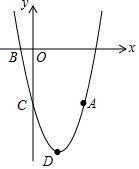 如图,抛物线y=ax2+bx-5(a≠0)经过点A(4,-5),与x轴的负半轴交于点B,与y轴交于点C,且OC=5OB,抛物线的顶点为点D.
如图,抛物线y=ax2+bx-5(a≠0)经过点A(4,-5),与x轴的负半轴交于点B,与y轴交于点C,且OC=5OB,抛物线的顶点为点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
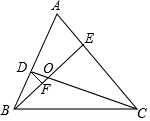 已知:如图,在等边△ABC中,点D、E分别在AB、AC上,且BD=AE,CD交BE于点O,DF⊥BE,点F为垂足.
已知:如图,在等边△ABC中,点D、E分别在AB、AC上,且BD=AE,CD交BE于点O,DF⊥BE,点F为垂足.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3(x+2)+12=4x | B. | 12(x+2)+12=12x | C. | 4(x+2)+12=3x | D. | 3(x+2)+1=4x |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com