
【题目】如图,已知矩形ABCD的周长为44cm,E是AD上的一点,F是AB上的一点,EF⊥EC,且EF=EC.

(1)若AF=6cm,求FC的长.
(2)连接BE,求证:BE平分∠ABC.
【答案】(1)![]() ;(2)详见解析.
;(2)详见解析.
【解析】
(1)根据矩形的性质易证△AEF≌△DCE (AAS),得到AE=DC,AF=DE,结合周长可求出AE,然后利用勾股定理求EF和FC即可;
(2)由(1)可得AE=AB,求出∠ABE=45°即可证明结论.
解:(1)∵四边形ABCD是矩形,
∴∠ABC=∠DCB=∠A=∠D=90°,AB=DC,
∴∠AEF+∠AFE=90°,
∵EF⊥EC,
∴∠FEC=90°,
∴∠AEF+∠DEC=90°,
∴∠AFE=∠DEC.
在△AEF和△DCE中,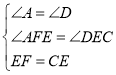 ,
,
∴△AEF≌△DCE (AAS).
∴AE=DC,AF=DE=6cm.
∵矩形ABCD的周长为44cm,
∴AD+DC=22cm.
∴AE+ED+DC=22cm.
∴2AE+AF=22cm.
∴2AE+6cm =22cm.
解得AE=8 cm.
在Rt△AEF中,FE=![]() ,
,
∴EF=EC=10.
在Rt△EFC中,FC=![]() ;
;
(2)由(1)得AE=DC,
∴AE=AB,
∴∠ABE=∠EBC=45°.
∴AE平分∠ABC.


科目:初中数学 来源: 题型:
【题目】如图,点 O 为数轴的原点,A,B 为数轴上两点,AB=15,且 OA=2OB.
![]()
(1)则点 A,B 表示的数分别为 , ;
(2)点 A,B 分别以 4 个单位长度/秒和 3 个单位长度/秒的速度相向而行,经过几秒后,A,B 两点相距 1 个单位长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
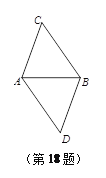
【题目】如图,将线段AB绕点A逆时针旋转α度角得到线段AC,将线段AB绕点B逆时针旋转α度角得到线段BD(0°<α<180°),连结BC、AD.当α=_______度时,四边形ACBD是菱形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形ABCD中,对角线AC、BD相交于点O,AE⊥BD,垂足为E,AD=8,
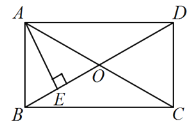
(1)若∠DAE︰∠BAE=3︰1,求∠EAC的度数;
(2)若ED=3BE,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠3,CD∥EF,试说明∠1=∠4.请将过程填写完整.

解:∵∠1=∠3,
又∠2=∠3(_______),
∴∠1=____,
∴______∥______(_______),
又∵CD∥EF,
∴AB∥_____,
∴∠1=∠4(两直线平行,同位角相等).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购买60件A商品和30件B商品共用了1080元,购买50件A商品和20件B商品共用了880元.
(1) A商品的单价是___________元,B商品的单价是___________元;
(2) 已知该商店购买B商品的件数比购买A商品的件数的2倍少4件,设购买A商品的件数为x件,该商店购买的A、B两种商品的总费用为y元.
① 求y与x的函数关系式.
② 如果需要购买A、B两种商品的总件数不少于32件,且该商店购买的A、B两种商品的总费用不超过296元,求购买B商品最多有多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在纸面上有一数轴(如图),折叠纸面.
![]()
(1)若表示1的点与表示![]() 的点重合,则表示
的点重合,则表示![]() 的点与表示 的点重合;
的点与表示 的点重合;
(2)若表示![]() 的点与表示3的点重合,回答以下问题:
的点与表示3的点重合,回答以下问题:
①表示5的点与表示 的点重合:
②若数轴上![]() 、
、![]() 两点之间的距离为14(
两点之间的距离为14(![]() 在
在![]() 的左侧),且
的左侧),且![]() 、
、![]() 两点经折叠后重合,求
两点经折叠后重合,求![]() 、
、![]() 两点表示的数是多少?
两点表示的数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在一次比赛中将所有参赛同学分为四个组,其中第一组有x人,第二组比第一组的![]() 少5人,第三组比第一、二组的和少15人,第一组的2倍与第四组的和是30人.
少5人,第三组比第一、二组的和少15人,第一组的2倍与第四组的和是30人.
(1)用含x的式子分别表示第二、三、四组的人数及参赛总人数;
(2)当x=10时,第四组与第三组相比,哪组的人数多?多多少人?
(3)x能否等于13,为什么?x能否等于20,为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com